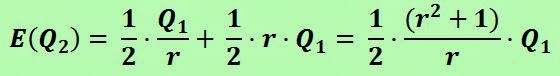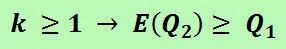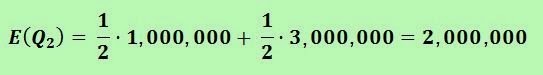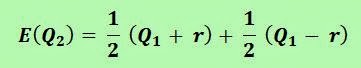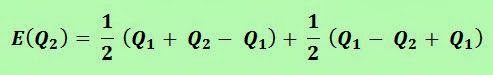(This post participates on the 109th edition of the Carnival of Mathematics, hosted by Tony's Maths blog.)
FIRST HALF
 It’s an awesome sunrise at a beautiful island in the South Pacific. It’s a place so far away from any inhabited place, that internet signal hardly arrives to it.
It’s an awesome sunrise at a beautiful island in the South Pacific. It’s a place so far away from any inhabited place, that internet signal hardly arrives to it.
Only every two hours, a telecommunications satellite passes over the island, and allows its inhabitants connect to the rest of the world just for a minute.
Michael Laudrup has chosen this idyllic place for a relaxing and deserved vacation with his family.
Like every morning, he has come to the sea-shore to witness the beautiful sunrise. It's eight o'clock. Just at this time the satellite passes over, and an incoming message sounds in his mobile.
 He doesn’t feel like picking up the phone, but he notices that it’s a message from his agent, so he finally decides to read it. The message says:
He doesn’t feel like picking up the phone, but he notices that it’s a message from his agent, so he finally decides to read it. The message says:
'Michael, you have 2 offers to coach next season. One is from Juventus, and the other is from Real Madrid. As you can see, one offer doubles the other.
The problem is that they need an immediate response, so within 2 hours, when you have connection again, you should answer and tell me which of the two teams you have decided to join. Otherwise, both teams will seek another coach. Juventus gives you 2 million euros per season, and Real Madrid...'
Damn! Just then, the satellite had gone enough away so that the connection is cut off.
 Michael had two hours to decide the team he will sign for.
Michael had two hours to decide the team he will sign for.So he went down to the beach, and began to think about the answer he would give to his manager.
Both offers came from two teams he had played for, so he didn’t feel a special predilection for one of them.
Juventus offer was very good, but… what if Real Madrid’s offer was better?
It would be a difficult decision. He could draw lots, but he thought that for such an important choice it's worth looking for a logical way to make the decision. Perhaps the little notions of the probability theory he still remembered from his younger times could help him...
Do you dare to help Michael to choose his new team for next season?
SECOND HALF
At the beginning, Laudrup thinks that Juventus offer is quite tempting. And besides, there is a 50% chance for his election to be the best offer.
 I would definitely like to earn this amount of money every year... And if he chooses the offer from Real Madrid it’s possible that he gets less money, so after two hours I would answer: I sign for Juventus!
I would definitely like to earn this amount of money every year... And if he chooses the offer from Real Madrid it’s possible that he gets less money, so after two hours I would answer: I sign for Juventus!Yes, it seems a logical choice.
Definitely. If by changing his choice he can earn 2 million more, and he can only lose 1 million, all is clear, right?
Well, here we would be facing an economics study on the marginal utility of these 2 million: Laudrup can be more concerned about losing 1 million than earning 2 more millions.
Nevertheless we'll assume that Michael cares the same an extra million he can win than a million he can lose, and we'll approach the problem from a mathematical point of view. Let's see: we have an offer of € 2,000,000 from Juventus, right?
Nevertheless we'll assume that Michael cares the same an extra million he can win than a million he can lose, and we'll approach the problem from a mathematical point of view. Let's see: we have an offer of € 2,000,000 from Juventus, right?
Yes.
And we know that one of the bids is twice the other. So Real Madrid may have offered 1 million or 4 million euros.
That's correct.
OK, now let's calculate what’s the expected amount of money Laudrup will get if he changes his mind and chooses joining Real Madrid.
There is a 50% chance of winning 1 million, and a 50% chance of winning 4 millions. So the expected gain of this second option, that we’ll call E(Q2), will be the average of the two possible cases:
So, if he swaps his choice, his expected return on swapping will be 2 and a half million euros on average, half a million more than if he signs for Juventus, right?
Indeed, if we apply the laws of probability, in this case Laudrup should choose the second option. But this fact doesn't only happen in this case, but in all cases, whenever the agent expresses the difference between the two offers in relative terms.
I don’t quite understand it.
We have 2 deals, Qa and Qb, and we define r as the ratio between the two offers:
We don’t care which of the two values, Qa or Qb, is the largest. In any case, r will always be a positive number greater than zero (for the moment, Laudrup is not thinking on coaching for free, so Qa and Qb aren’t zero, nor is thinking in paying money for it, so Qa and Qb are two positive values greater than zero).
If we call Q1 to the offer we take first, and Q2 to the offer we have rejected, we have that the value of Q2 can be (Q1 · r) or (Q1 / r).
We calculate the expected value of Q2, which we call E(Q2), for the case that all the offers are equally likely of being the greatest one:
We define k as
We have that
Let's see graphically how the value of k behaves according to the values of r, that is, depending on the difference between the two offers:

We can see that k is always greater than 1, except when the two offers are equal, so the expected value of the unknown offer E(Q2) is always greater than the one we know Q1. That way, we should always choose the latter offer.
Then, Laudrup will answer: I sign for Real Madrid!
Yes, but… can you imagine what would happen if his agent had mentioned in the first place the Real Madrid’s offer? Following the same reasoning, now Laudrup would be signing for Juventus…
However, we find this paradox only when the relationship between the two offers is expressed in relative terms. But imagine that his agent, instead of saying that an offer doubles the other, says that an offer is greater than the other in € 1,000,000 for example, that is, he quantifies the difference in absolute values. What happens then?
I don’t know.
We can recalculate the expected gain if Laudrup chooses Real Madrid’s offer:
It turns out that he obtains an expected gain of € 2,000,000, just the same amount offered by Juventus!
Let's see it in mathematical terms. If we now define r as:
we get:
So if we express the difference in absolute terms, not relative, it happens that we get a more 'logical' mathematical solution...
That’s true, in this case the mathematical result matches with what common sense dictates.

It's a hard time to decide on one of the 2 teams, because we estimate that both offers are equal, and because he has the same sympathy for both teams, so Michael will probably say: I stay in my current team!
Well, such opportunities don’t come around every day. Can’t we help him in some way to decide on an offer?
OK, after all these calculations, we're not going to leave him without a solution to his problem.
We’ve seen that according to how we interpret the data, the decision may be different. What should Laudrup do to take a right decision?

Do you remember when Llorente didn’t know what to do, if signing for Tottenham Hotspur or Aston Villa? We saw it a while ago in our story ‘Llorente's hard decision’.
Ah, yes, I remember it. In that case what we had to do was applying the theory of optimal stopping, right?
That’s right. The first thing Laudrup has to do is thinking about how much money wants to earn by coaching next season, and when he picks an offer that equals or exceeds that amount, he must take it, without thinking that there may be better deals. And since the offer of Juventus seemed interesting enough and meets his expectations, he should definitely take it.

So we can conclude that Laudrup’s answer will be: I sign for Juventus!
Sorry, but it will not be so!
How? Is there any other reasoning that we haven’t considered?
Surely. This issue has a direct relationship with theory of decision and Bayesian interpretation of probability, and it has been studied for a long time by experts in logic, philosophy, mathematics, etc. It’s called ‘the two envelopes paradox’ or ‘the paradox of change’. On these links you can find more information about this paradox: The Two-Envelope Problem Solution: Part I, The Two-Envelope Problem Solution: Part II, The Two Envelopes Problem.
Yes, but at the end, what was Laudrup’s choice? You’ve mentioned that he rejected the offers of both teams.
Certainly, after 2 hours walking on the beach, he decided that neither in Madrid nor in Turin he could see such gorgeous sunrises as on this island. And he decided that he will no longer coach his team again. He’ll take a year off, resting in this magnificent place with his family.
And after sending the reply message to his agent, he did what he should have done when he came to the island: he turned off the phone.