Weidenfeller, Grosskreutz and Schieber are Borussia Dortmund players.
They wear on their backs number 1, 19 and 23, respectively.
They’ve just lost the Champions League final at Wembley, but they are happy.
Lahm, Boateng and Javi Martinez are Bayern Munich players.
They wear on their backs number 21, 17 and 8, respectively.
They just won the Champions League final at Wembley, but they’re not happy.
Can you imagine what happens here?
Perhaps, you’ll think: Well, I can understand Borussia players: I guess that reaching a continental final is a thing to be proud of, although having lost it.
No doubt, this is a very important sporting achievement, but this sort of things is better valued after a while than some minutes after losing the final.
Maybe Borussia players are considering their incentive bonus for having reached the final ...
Although the premium is not inconsiderable, certainly they’d change the bonus for winning the title.
Possibly they are now thinking about their holidays ...
That’s a good reason to be happy, but ... what about Bayern players?
They’ve just won the Champions League, they will receive a great bonus, and they'll go on vacation too...
It's true. So which is the explanation?
Very simple: because Borussia Dortmund players carry happy numbers, and Bayern Munich players wear unhappy numbers on their shirts.
Are there happy and unhappy numbers?
Yes, there are.
And what things distinguishes one happy number from an unhappy one?
Well, in Mathematics, happy numbers are defined as follows: choose one number and calculate the sum of the squares of its digits. With the result, repeat the process until the sum equals 1, or until we enter an infinite cycle that will never reach number 1.
Following this process, the numbers that end in number 1, are called 'happy numbers', while the numbers that enter in a loop are known as 'unhappy (or sad) numbers'.
Let's see an example of happy number:
And now let's see an example of unhappy (or sad) number:
You can see that, after obtaining number 4, we've entered in a loop of numbers
In mathematical form, we stand that: Given a number n = n0, define a sequence n1, n2, ... where ni+1 is the sum of the squares of the digits of ni. Then n is happy if and only if there exists i such that ni=1.
Thus, the first happy numbers are:


Also, if a number is happy, then all members of the sequence of results generated are also happy. And if a number is unhappy, the whole sequence of numbers generated by applying the procedure will be also unhappy.
Thus, in the second example, we can determine not only number 11 is unhappy, but also numbers 2, 4, 16, 37, 58, 89, 145, 42 and 20 are unhappy ...
Indeed, from a happy number we’ll obtain a lot of additional happy numbers, by inserting zeroes among its digits, or changing the order of its digits: 2, 4, 16, 37, 58, 89, 145, 42 and 20.
And, why are so called, and what is their use?
It's not known the origin of its name. Perhaps they are happy because they finally reach their goal (the number 1), while the unhappy are doomed to wander forever through space mathematical ...
Their usefulness..., so far nothing but mathematical entertainment to practice with the exponentiation, but perhaps in the future we will find some practical application. Want to try?
If you want to learn more about happy numbers, you can see on the Wikipedia or on the web Articles for education












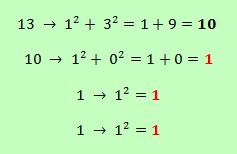

What is the probability that a randomly chosen integer is happy? We can answer this for a range of integers and get the frequency approach solution. Is there a classical probability way?
ReplyDelete