FIRST HALF
It's been an awful summer for Klaus Händler.
Klaus is a football agent, and during the last months none of the transfers that he has negotiated has come to a successful conclusion.
Some clubs he works with have no money for signing new players because of the economic crisis, and moreover, some of the players he represents are injured.
He's thinking he'll have to sell some of his dearest Lamborghini cars to afford the expenses of his comfortable life style during this winter, while, suddenly, the phone rings.

It's Josef, chairman of the FC Schalke 04:
- Klaus, just now we've got 5 forwards in our team, and we want to transfer one of them. Could you take charge of it?
Just after hanging up the phone, it rings again. This time it's Michael, chairman of the Bayer 04 Leverkusen:
- Klaus, how are you? I call you because today is the transfer deadline day, and we want to sign one additional forward...
It looks like Klaus won't have to sell his luxury cars...
But there's a problem. Both teams are interested in increasing the average goal-scoring ability of their forward line and, at the same time, reducing the average wage of their players.
Klaus phones some teams, to see if it's possible any agreement, but all the teams have completed their playing staffs.
It seems clear that it's not possible to transfer a forward from Schalke to Bayer, because of the imposed conditions by both teams. So, what can Klaus do? Could we help him in some way?
SECOND HALF

Klaus has decided to call his friend Joe Vitruvius, to see if he can help with this apparently unsolvable problem.
- Joe, I think that if we transfer one player from Schalke 04 to Bayer Leverkussen, the goal-scoring average of Bayer will rise at the same rate as Schalke's average decreases. And, in same way, the average wage of Bayer will go up at the same rate as the Schalke's average goes down.
- So, you think that everything a team gets, the other loses it. That's what we know as zero-sum game in mathematical game theory. But it's not always like this. As in real life, we can find situations in which all parts win or lose (non-zero-sum games).
- Yes, but I don't think this is one of the times it works.
- Well, we can try it. You told me that both teams want to increase the average goal-scoring ability of their forward line, and at the same time, reduce their average wage, didn't you?

- Yes, that's right.
- if we talk in absolute values, there's no way of doing it. But as we talk about averages, it may be possible. Can you give me the data of goals and salaries of the forwards of the two teams?
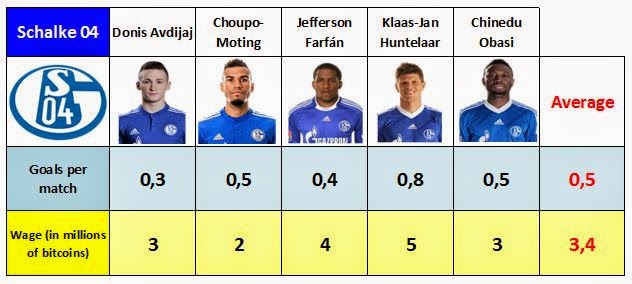
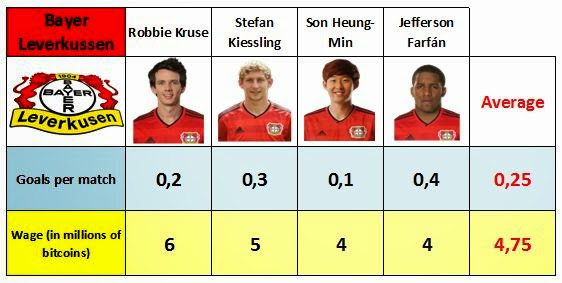
- Yes, of course. Here you are.
- Well, let's calculate the means of goals and wages of both forward lines.
- Now we can verify if there's a solution for your problem. We only have to apply the Will Rogers phenomenon.

- And... what's that about?
- This paradox is related to a comment that Will Rogers, an American artist, said in the early 20th century: “When the Okies left Oklahoma and moved to California, they raised the average intelligence level in both states".
- He meant that when the citizens from Oklahoma move to California are the less intelligent persons of their state, even so they're more intelligent than California inhabitants, right?
- That's right. This way, any inhabitant from Oklahoma whose intelligence is under the state average, that moves to California, makes that the average intelligence levels of both states experience an increment.
- And how can we apply it to our case?
- Well. Let's look at the Schalke 04 player, the Peruvian Jefferson Farfán. His goal-scoring ability is smaller than the team's average, but his salary is higher than his teammates average. However, he scores more goals than Bayer Leverkussen's forwards, and earns less money than them.
- I understand. If we transfer the player from one team to the other, assuming that he will earn the same, and that he will score the same goals, both teams will improve their statistics.
- That's right. Let's see how it works on the table.
- Indeed, both teams have improved their average goal-scoring level, and have reduced their average wages. And does this happen always?

- No, not ever. But sometimes it does, like in this case.
- Well, you've just solved my economics this winter. I would have to invite you to a good meal…
- I think this will cost you more than a simple meal. I prefer we do the following deal: you'll pay me in function of the goals that Jefferson scores this season. If he scores only one goal, you'll pay me 2 bitcoins. If he scores 2, you'll double the amount, 4 bitcoins. If he scores 3 goals, I will receive the double, that is, 8 bitcoins. And so on.
- That seems a fair deal. I agree.
The transfer was done. Schalke sold one of its excedent players, Bayer signed an extraordinary forward, and Klaus didn't have to get rid of his precious Lamborghini automobiles. At least during this winter, because Farfán scored 25 goles for his new team…
Can you calculate how many bitcoins Joe Vitruvius received from Klaus Händler at the end of the football season?
If you're interested in learning more about this topic of the Will Rogers phenomenon and about the game theory, you can visit any of this magnific articles: The "Will Rogers Phenomenon" lets you save lives by doing nothing, The Will Rogers phenomenon, Game Theory and the Nash Equilibrium, Evolutionary Game Theory, Advanced Game Theory Overview,

Below this lines you will find other links, for if you liked this story and you want to share it with your friends.
And don't forget to take a walk by the Carnival of Mathematics. There you'll find lots of excellent math posts that you'll surely like too.