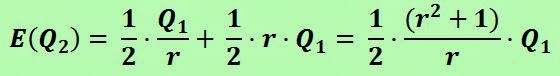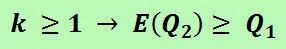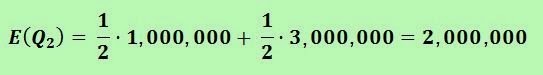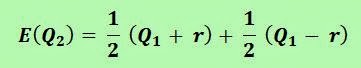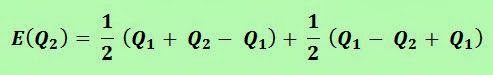An impossible transfer

A football agent burdened by failing to make any transfer during the summer, suddenly comes across a unique opportunity. The problem is that the acquiring team and the selling team have seemingly opposing interests. Will he be able to please both sides? The Will Rogers phenomenon and the game theory.

FIRST HALF

It's been an awful summer for Klaus Händler.

Klaus is a football agent, and during the last months none of the transfers that he has negotiated has come to a successful conclusion.

Some clubs he works with have no money for signing new players because of the economic crisis, and moreover, some of the players he represents are injured.

He's thinking he'll have to sell some of his dearest Lamborghini cars to afford the expenses of his comfortable life style during this winter, while, suddenly, the phone rings.

It's Josef, chairman of the FC Schalke 04:

- Klaus, just now we've got 5 forwards in our team, and we want to transfer one of them. Could you take charge of it?

Just after hanging up the phone, it rings again. This time it's Michael, chairman of the Bayer 04 Leverkusen:

- Klaus, how are you? I call you because today is the transfer deadline day, and we want to sign one additional forward...

It looks like Klaus won't have to sell his luxury cars...

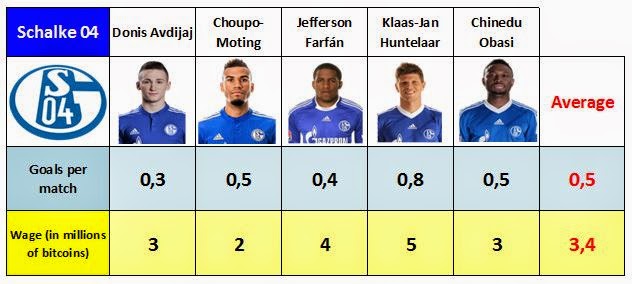
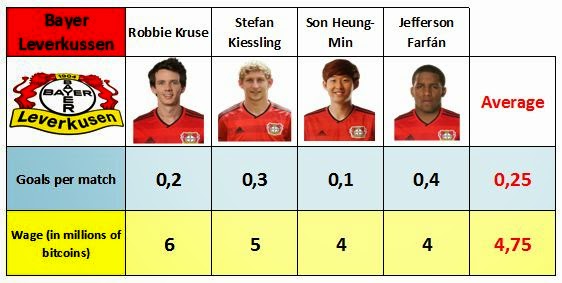
But there's a problem. Both teams are interested in increasing the average goal-scoring ability of their forward line and, at the same time, reducing the average wage of their players.

Klaus phones some teams, to see if it's possible any agreement, but all the teams have completed their playing staffs.

It seems clear that it's not possible to transfer a forward from Schalke to Bayer, because of the imposed conditions by both teams. So, what can Klaus do? Could we help him in some way?

SECOND HALF

Klaus has decided to call his friend Joe Vitruvius, to see if he can help with this apparently unsolvable problem.

- Joe, I think that if we transfer one player from Schalke 04 to Bayer Leverkussen, the goal-scoring average of Bayer will rise at the same rate as Schalke's average decreases. And, in same way, the average wage of Bayer will go up at the same rate as the Schalke's average goes down.

- So, you think that everything a team gets, the other loses it. That's what we know as zero-sum game in mathematical game theory. But it's not always like this. As in real life, we can find situations in which all parts win or lose (non-zero-sum games).

- Yes, but I don't think this is one of the times it works.

- Well, we can try it. You told me that both teams want to increase the average goal-scoring ability of their forward line, and at the same time, reduce their average wage, didn't you?

- Yes, that's right.

- if we talk in absolute values, there's no way of doing it. But as we talk about averages, it may be possible. Can you give me the data of goals and salaries of the forwards of the two teams?

- Yes, of course. Here you are.

- Well, let's calculate the means of goals and wages of both forward lines.

- Now we can verify if there's a solution for your problem. We only have to apply the Will Rogers phenomenon.

- And... what's that about?

- This paradox is related to a comment that Will Rogers, an American artist, said in the early 20th century: “When the Okies left Oklahoma and moved to California, they raised the average intelligence level in both states".

- He meant that when the citizens from Oklahoma move to California are the less intelligent persons of their state, even so they're more intelligent than California inhabitants, right?

- That's right. This way, any inhabitant from Oklahoma whose intelligence is under the state average, that moves to California, makes that the average intelligence levels of both states experience an increment.

- And how can we apply it to our case?

- Well. Let's look at the Schalke 04 player, the Peruvian Jefferson Farfán. His goal-scoring ability is smaller than the team's average, but his salary is higher than his teammates average. However, he scores more goals than Bayer Leverkussen's forwards, and earns less money than them.

- I understand. If we transfer the player from one team to the other, assuming that he will earn the same, and that he will score the same goals, both teams will improve their statistics.

- That's right. Let's see how it works on the table.

- Indeed, both teams have improved their average goal-scoring level, and have reduced their average wages. And does this happen always?

- No, not ever. But sometimes it does, like in this case.

- Well, you've just solved my economics this winter. I would have to invite you to a good meal…

- I think this will cost you more than a simple meal. I prefer we do the following deal: you'll pay me in function of the goals that Jefferson scores this season. If he scores only one goal, you'll pay me 2 bitcoins. If he scores 2, you'll double the amount, 4 bitcoins. If he scores 3 goals, I will receive the double, that is, 8 bitcoins. And so on.

- That seems a fair deal. I agree.

The transfer was done. Schalke sold one of its excedent players, Bayer signed an extraordinary forward, and Klaus didn't have to get rid of his precious Lamborghini automobiles. At least during this winter, because Farfán scored 25 goles for his new team…

Can you calculate how many bitcoins Joe Vitruvius received from Klaus Händler at the end of the football season?

If you're interested in learning more about this topic of the Will Rogers phenomenon and about the game theory, you can visit any of this magnific articles: The "Will Rogers Phenomenon" lets you save lives by doing nothing, The Will Rogers phenomenon, Game Theory and the Nash Equilibrium, Evolutionary Game Theory, Advanced Game Theory Overview,

Below this lines  you will find other links, for if you liked this story and you want to share it with your friends.

And don't forget to take a walk by the Carnival of Mathematics. There you'll find lots of excellent math posts that you'll surely like too.

Probability and sunrise

It's easy to choose between some options when you know all about them. But when not all data are available, it turns quite difficult to find a satisfactory way of making a decision. In this case, Michael Laudrup faces a decision among two offers, but he only knows the conditions of one of them. And when he tries to solve the problem through a mathematical procedure, he gets even more confused about the choice. Do you know anything about the exchange paradox?

(This post participates on the 109th edition of the Carnival of Mathematics, hosted by Tony's Maths blog.)

FIRST HALF

It’s an awesome sunrise at a beautiful island in the South Pacific. It’s a place so far away from any inhabited place, that internet signal hardly arrives to it.

Only every two hours, a telecommunications satellite passes over the island, and allows its inhabitants connect to the rest of the world just for a minute.

Michael Laudrup has chosen this idyllic place for a relaxing and deserved vacation with his family.

Like every morning, he has come to the sea-shore to witness the beautiful sunrise. It's eight o'clock. Just at this time the satellite passes over, and an incoming message sounds in his mobile.

He doesn’t feel like picking up the phone, but he notices that it’s a message from his agent, so he finally decides to read it. The message says:

'Michael, you have 2 offers to coach next season. One is from Juventus, and the other is from Real Madrid. As you can see, one offer doubles the other.

The problem is that they need an immediate response, so within 2 hours, when you have connection again, you should answer and tell me which of the two teams you have decided to join. Otherwise, both teams will seek another coach. Juventus gives you 2 million euros per season, and Real Madrid...'

Damn! Just then, the satellite had gone enough away so that the connection is cut off.

Michael had two hours to decide the team he will sign for.

So he went down to the beach, and began to think about the answer he would give to his manager.

Both offers came from two teams he had played for, so he didn’t feel a special predilection for one of them.

Juventus offer was very good, but… what if Real Madrid’s offer was better?

vs.

It would be a difficult decision. He could draw lots, but he thought that for such an important choice it's worth looking for a logical way to make the decision. Perhaps the little notions of the probability theory he still remembered from his younger times could help him...

Do you dare to help Michael to choose his new team for next season?

SECOND HALF

At the beginning, Laudrup thinks that Juventus offer is quite tempting. And besides, there is a 50% chance for his election to be the best offer.

I would definitely like to earn this amount of money every year... And if he chooses the offer from Real Madrid it’s possible that he gets less money, so after two hours I would answer: I sign for Juventus!

Yes, it seems a logical choice.

Definitely. If by changing his choice he can earn 2 million more, and he can only lose 1 million, all is clear, right?

Well, here we would be facing an economics study on the marginal utility of these 2 million: Laudrup can be more concerned about losing 1 million than earning 2 more millions.

Nevertheless we'll assume that Michael cares the same an extra million he can win than a million he can lose, and we'll approach the problem from a mathematical point of view. Let's see: we have an offer of € 2,000,000 from Juventus, right?

Yes.

And we know that one of the bids is twice the other. So Real Madrid may have offered 1 million or 4 million euros.

That's correct.

OK, now let's calculate what’s the expected amount of money Laudrup will get if he changes his mind and chooses joining Real Madrid.

There is a 50% chance of winning 1 million, and a 50% chance of winning 4 millions. So the expected gain of this second option, that we’ll call E(Q₂), will be the average of the two possible cases:

So, if he swaps his choice, his expected return on swapping will be 2 and a half million euros on average, half a million more than if he signs for Juventus, right?

Indeed, if we apply the laws of probability, in this case Laudrup should choose the second option. But this fact doesn't only happen in this case, but in all cases, whenever  the agent expresses the difference between the two offers in relative terms.

I don’t quite understand it.

We have 2 deals, Q_a and Q_b, and we define r as the ratio between the two offers:

We don’t care which of the two values, Q_a or Q_b, is the largest. In any case, r will always be a positive number greater than zero (for the moment, Laudrup is not thinking on coaching for free, so Q_a and Q_b aren’t zero, nor is thinking in paying money for it, so Q_a and Q_b are two positive values greater than zero).

If we call Q₁ to the offer we take first, and Q₂ to the offer we have rejected, we have that the value of Q₂ can be (Q₁ · r) or (Q₁ / r).

We calculate the expected value of Q₂, which we call E(Q₂), for the case that all the offers are equally likely of being the greatest one:

We define k as

We have that

Let's see graphically how the value of k behaves according to the values of r, that is, depending on the difference between the two offers:

We can see that k is always greater than 1, except when the two offers are equal, so the expected value of the unknown offer E(Q₂) is always greater than the one we know Q₁. That way, we should always choose the latter offer.

Then, Laudrup will answer: I sign for Real Madrid!

Yes, but… can you imagine what would happen if his agent had mentioned in the first place the Real Madrid’s offer? Following the same reasoning, now Laudrup would be signing for Juventus…

However, we find this paradox only when the relationship between the two offers is expressed in relative terms. But imagine that his agent, instead of saying that an offer doubles the other, says that an offer is greater than the other in € 1,000,000 for example, that is, he quantifies the difference in absolute values. What happens then?

I don’t know.

We can recalculate the expected gain if Laudrup chooses Real Madrid’s offer:

It turns out that he obtains an expected gain of € 2,000,000, just the same amount offered by Juventus!

Let's see it in mathematical terms. If we now define r as:

we get:

So if we express the difference in absolute terms, not relative, it happens that we get a more 'logical' mathematical solution...

That’s true, in this case the mathematical result matches with what common sense dictates.

It's a hard time to decide on one of the 2 teams, because we estimate that both offers are equal, and because he has the same sympathy for both teams, so Michael will probably say: I stay in my current team!

Well, such opportunities don’t come around every day. Can’t we help him in some way to decide on an offer?

OK, after all these calculations, we're not going to leave him without a solution to his problem.

We’ve seen that according to how we interpret the data, the decision may be different. What should Laudrup do to take a right decision?

Do you remember when Llorente didn’t know what to do, if signing for Tottenham Hotspur or Aston Villa? We saw it a while ago in our story ‘Llorente's hard decision’.

Ah, yes, I remember it. In that case what we had to do was applying the theory of optimal stopping, right?

That’s right. The first thing Laudrup has to do is thinking about how much money wants to earn by coaching next season, and when he picks an offer that equals or exceeds that amount, he must take it, without thinking that there may be better deals. And since the offer of Juventus seemed interesting enough and meets his expectations, he should definitely take it.

So we can conclude that Laudrup’s answer will be: I sign for Juventus!

Sorry, but it will not be so!

How? Is there any other reasoning that we haven’t considered?

Surely. This issue has a direct relationship with theory of decision and Bayesian interpretation of probability, and it has been studied for a long time by experts in logic, philosophy, mathematics, etc. It’s called ‘the two envelopes paradox’ or ‘the paradox of change’. On these links you can find more information about this paradox: The Two-Envelope Problem Solution: Part I, The Two-Envelope Problem Solution: Part II, The Two Envelopes Problem.

Yes, but at the end, what was Laudrup’s choice? You’ve mentioned that he rejected the offers of both teams.

Certainly, after 2 hours walking on the beach, he decided that neither in Madrid nor in Turin he could see such gorgeous sunrises as on this island. And he decided that he will no longer coach his team again. He’ll take a year off, resting in this magnificent place with his family.

And after sending the reply message to his agent, he did what he should have done when he came to the island: he turned off the phone.

Si te gustó esta historia, puedes votar por ella en menéame y divoblogger. Muchas gracias.