Trees and googols at World Cup 2014

A new mathematical cocktail whose stars are the World Cup in Brazil, the different systems of competition, the number of Wedderburn-Etherington and tree topology.

(This post participes on the 111th edition of the Carnival de Mathematics, hosted by the blog Boole's Rings.)

FIRST HALF

There’s a great commotion few days before the start of the Football World Cup Brazil 2014. The organizing committee has decided to introduce an amendment at the last minute.

They want to add more countries to t he 32 nationsalready qualified for the final tournament. There’re many national teams that have been left out of the championship.

Given the huge stir generated by this World Championship, and the disappointment of many countries for failing to qualify, World Cup organizers have decided to increase the number of participants.

The competition system initially established for the 32 countries was as follows: a first stage based on a league format with 8 groups of 4 countries, the first 2 teams of which qualify for next round.

The 16 teams qualified will meet on 3 knockout stages till the final, where the winner will take the World Cup.

However, if they want to add more countries, and achieve a not over-extended championship, they must necessarily adopt a new competition format, discarding the initial leagues and performing a knockout format from the beginning.

Moreover, given the availability of the football stadiums and the logistical problems that may result from this modification, they have determined to bring the 64 matches originally listed with the old system down to 60 games.

The Local Organizing Committee has called a meeting with several experts from the Department of Applied Mathematics of the Ministry of Education.

At this meeting, the Committee chairman exposes to the other attendees the couple of issues that arise:

- The first issue consists on to determine the maximum number of teams that can participate if a total of 60 matches are held. We want the highest number of countries to come, because, first, we will have more visits of tourists from the participating countries, and second, we will have more income from television rights of those who choose to watch it at home.

- The second one is to analyze how many different ways we can arrange the tournament with knockout matches.

- What do you mean exactly?

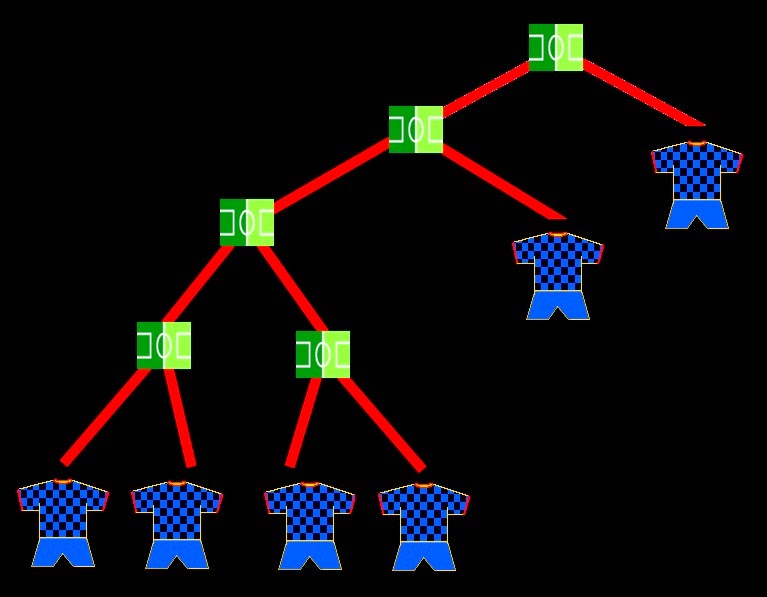
- I mean that the championship can be played in many ways. For example, we can establish that there are 8 seeded teams, and make the other countries compete until there're only 8 teams to meet them in round of 16. Thus, if we represent the matches to dispute as small green rectangular stadiums, and teams with a blueish soccer clothing, our competition diagram looks like this: 

- Or we can choose only 4 seeded teams and the rest are eliminated until there're only 4 national teams to face them.

- Or we set just 1 seeded team (the host country, of course), and the rest are eliminated until there is only one to play the final with us. Anyway, all the variations you can think of.

- I understand. But... it won’t be possible... It's a lot of work... for so little time.

- I don’t want excuses. Come on, let's get to work, and we’ll meet here again tomorrow.

The head of the Applied Mathematics Department is very concerned about these questions. Can you help him?

SECOND HALF

The following day, the mathematical experts meet again the members of the Organizing Committee.

- We'll try to solve the first question. What do you think about it? What’s the maximum number of countries we can call if 60 matches are held?

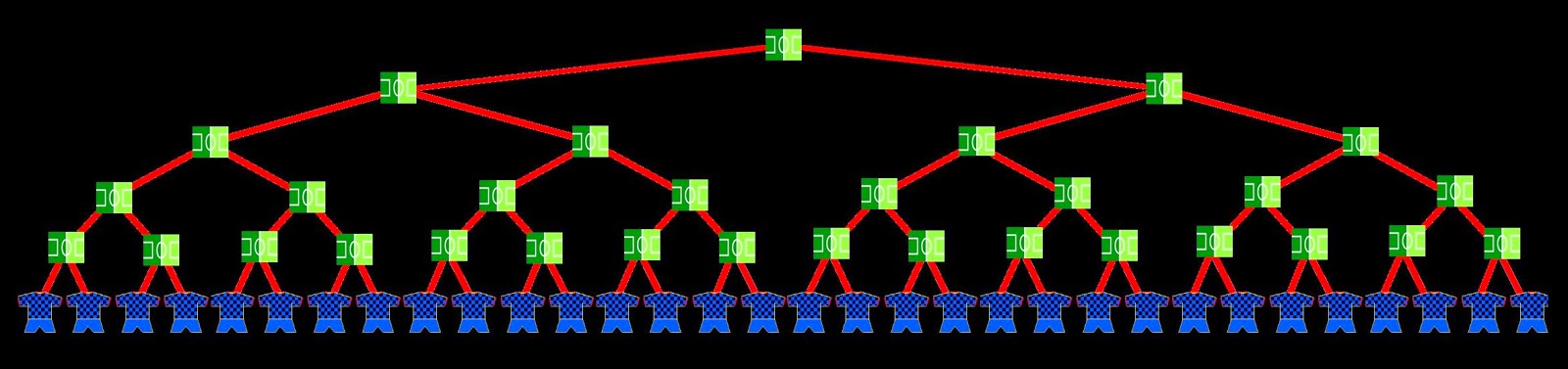
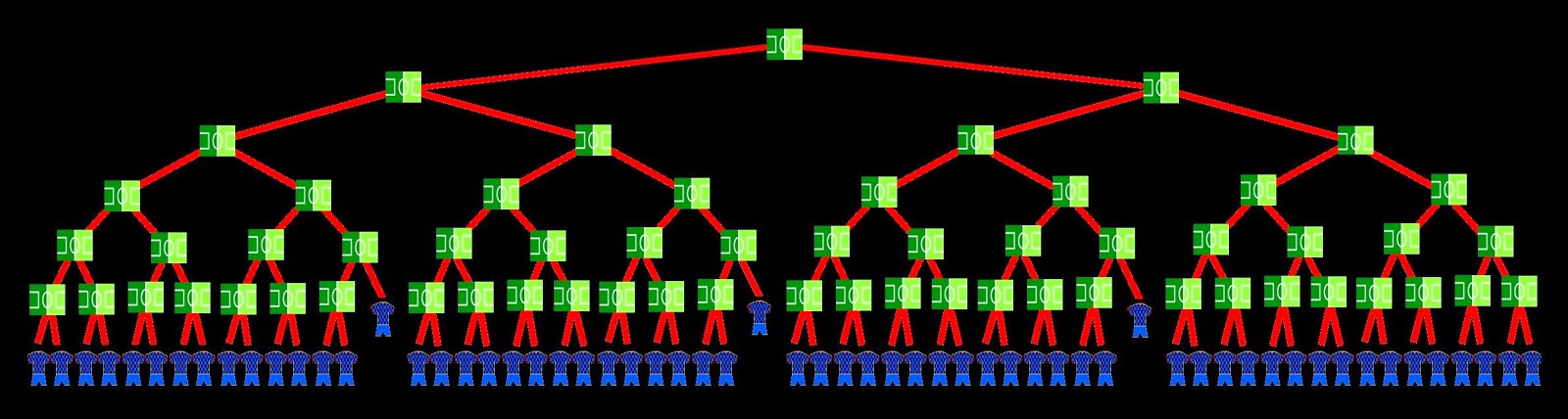
- Well, I think the best will be to make a match plan, as in tennis tournaments. We’ll represent the final match with a small soccer field, and we’ll draw 2 lines from it, to the two teams that will play the match. We have 1 match.

- Now we replace the shirts representing the teams with 2 pitches symbolizing the 2 semifinal matches. From each of them we draw another 2 lines, with the teams who play the matches. And if we add these 2 new matches to the one of the final, we already have 3 matches in total.

- And we go on with the 4 quarter-final matches, the 8 round of 16 matches and the 16 round of 32 matches. We now have a total of 1+2+4+8+16 = 31 matches.

- We still need 29 more games to complete the 60 matches we want to be played in the championship. So we can’t hold all the 32 matches of round of 64, since we would have a total of 31 + 32 = 63 games. You can count the soccer pitches in the scheme, to check it.

- 3 matches are left over. So we remove 3 matches, and there’ll be 3 teams directly qualified for the round of 32.

- Now let's count the teams participating in the tournament: we must count all the shirts hanging like leaves at the ends of each branch.

- It's true, the diagram of the tournament looks like a tree. Well, after counting them, I get 61, that is, we can hold up to 61 countries, right?

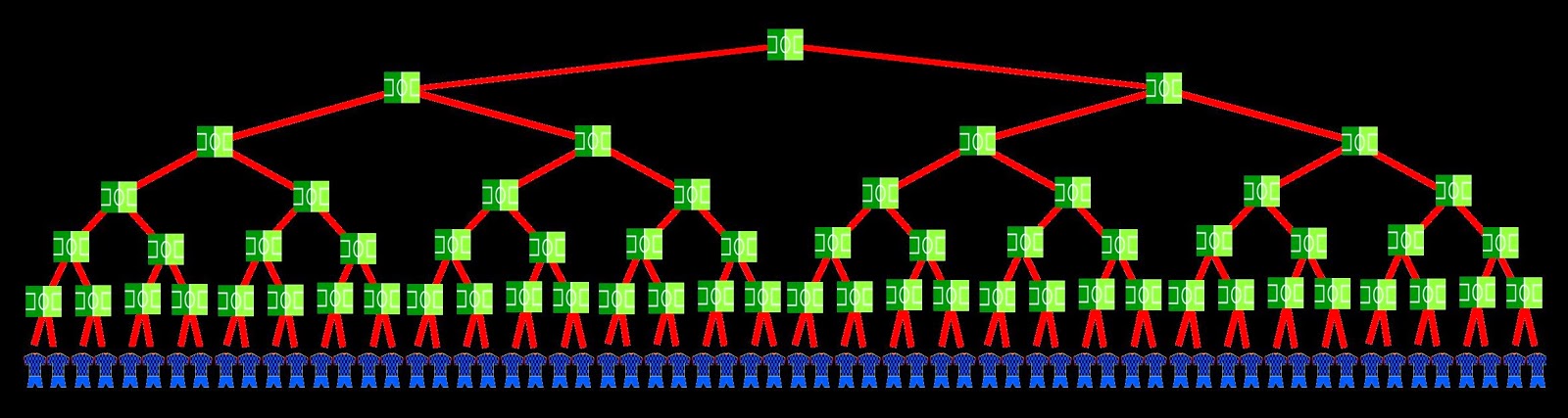
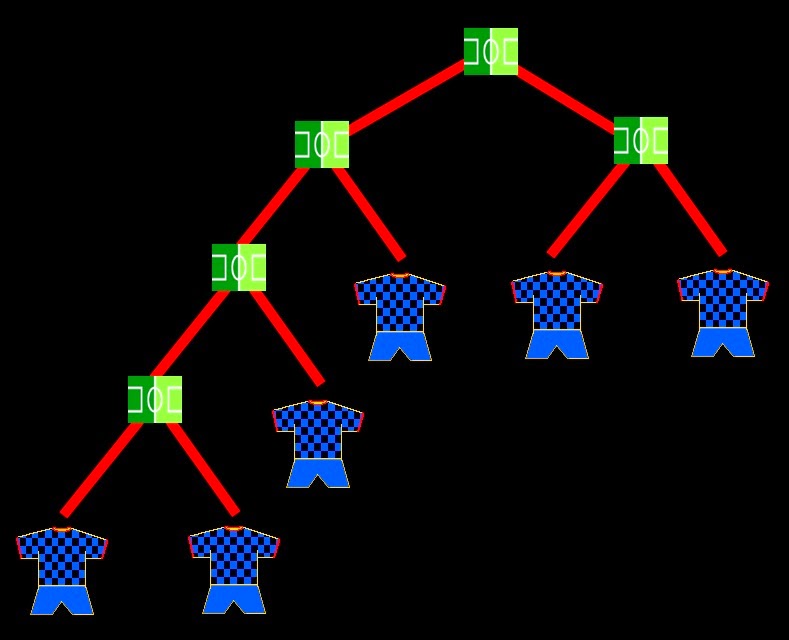
- That's right, whenever the tournament is arranged with this competition scheme. But what about if we manage another distinct trees? If we want to have 8 top seeded teams, or if we want to have 4 seeded teams, always respecting the number of 60 games, the trees would be:

- What now? Will be there more or less countries this way? And what about if we think on other different trees?

- We can see that in these two examples we get also 61 countries, but I don't know what would happen to the rest of trees we can design... 

- We’ll always get 61 countries, and we’ll use to a curious procedure to prove it.

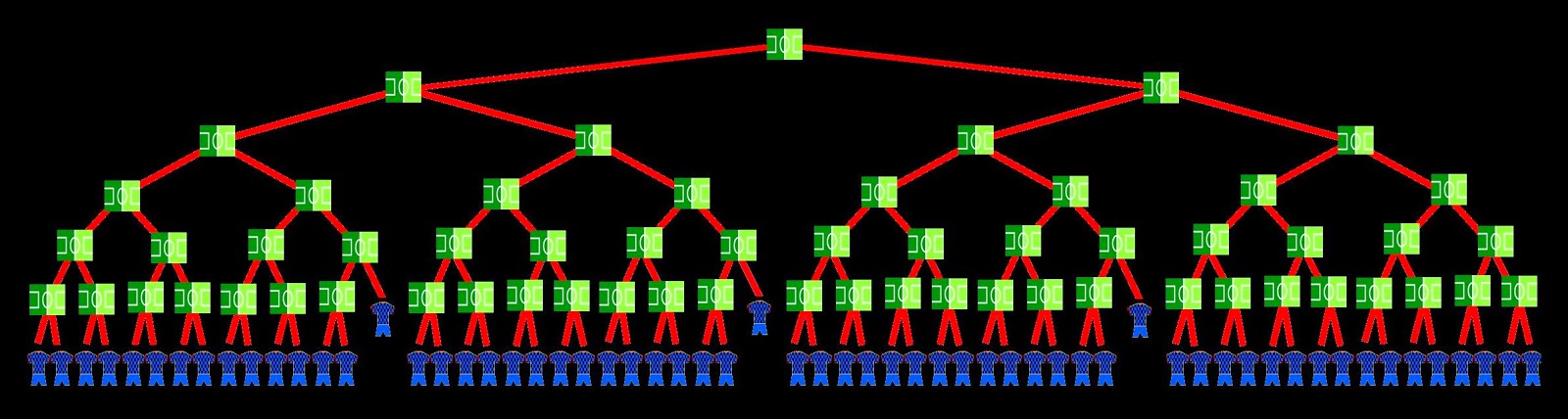
- Let's think about the following: in all knockout games, there will always be a loser, that no longer will play more games. We just have to think that in 60 matches there will be 60 ‘losers’  countries, whom we have to add the final winner. Therefore, there will be 61 countries, regardless of the form the competition schedule takes.

-We can look at it in another way: if in every game we have represented a football pitch, we state that the team that wins the match and moves to the next phase occupies the darker half, while the loser is set in the lighter green part, we can see  that there are 60 clearer parts corresponding to the 60 eliminated teams, to which it must be added the team that wins the tournament, who has always been on the dark area of its matches. So we have a total of 61 teams. And it doesn’t matter the 'tree' of the competition that we form.

- It's true. So we can say that the first question of finding the maximum number of countries is solved.

- Now let's study the second question: how many different ways we can arrange the tournament. In other words, we have to evaluate the distinct trees that we can design to organize the championship with 61 countries.

- Well, it doesn't seem very difficult. Let's start with a championship without teams. With zero participants, we could not organize any championship, right? 

- Now consider a one-team championship. It's very easy. There’is only one way to do it: just give the trophy to the one team, and that's it.

- With 2 teams, both would play the final. There would only be one way to organize it.

- Correct.

- With 3 teams, there’s also only one possible way to arrange the event: first we bring together 2 teams, and then the winner plays with the third team, right?

- Indeed. But if instead of bringing together the first and the second team, we make the first and the third team face each other, or the second and the third, then we have two additional arrangements, right?

- No. It’s true that the teams would be different, but the pattern of competition would be the same: at first, 2 teams play a match, and the winner plays with the remaining team. For now, what we want is to find out how many distinct match schedules we can make and decide for one of them. Then we'll see how to put each of the national teams within that scheme, okay? So we’ll go on painting all teams with the same color.

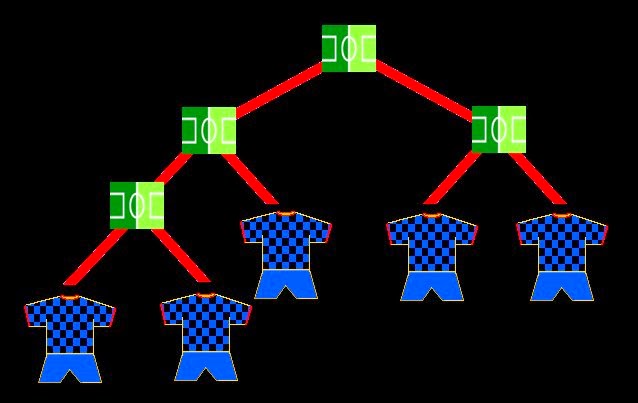
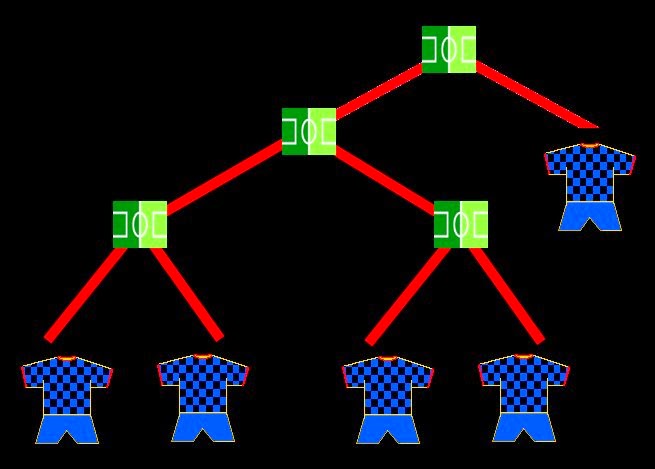
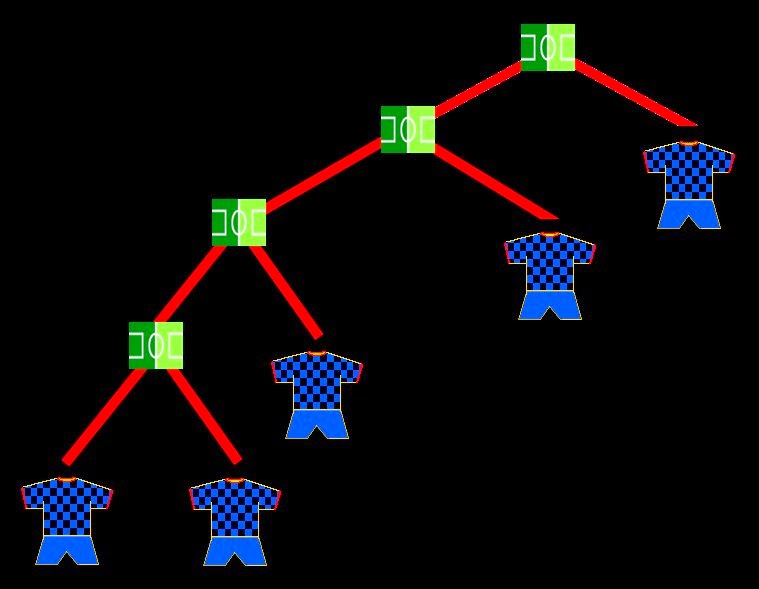
- Perfect. Now we'll work with 4 teams. The most usual is to make them confront each other on 2 semifinals, and the winners play the final.

- But there’s another way to deal with them: eliminating one by one.

- So with 4 teams, we have 2 different trees. Let's see with 5 teams: there are 3 possible schemes.

- And with 6 teams, I can think of 6 possible ways.

- With 7 teams we can form 11 different trees. With 8 we build 23 trees, and with 9 we can design 46 trees. But it's increasingly difficult to draw the different options. I think this way we won't get anywhere... 

- Maybe we should find a formula to calculate how many distinct trees can be formed with 61 competitors. To do this, we'll study the series we have so far, to see if we can deduce how it follows.

- It doesn’t seem that the numbers we’ve obtained obey any mathematical sequence. Maybe we should search on internet for a solution to our problem.

- Yes, but the first thing we have to do is to define exactly what we're looking for.

- Well, these trees we're drawing are called 'graphs' in mathematical terms. And as they have a hierarchical form, which simulates a tree (or a root), they’re also known by the name of ‘trees’ in Mathematics and Computer science.

- In addition, these trees are very special because from all of those little pitches (which we call nodes) representing the football matches, we start 2 lines (branches or children). There can’t be a game in which more than 2 teams meet, so we talk about ‘binary trees’. And no match can be played with only one team, so therefore, we say they’re  'strictly binary trees’.

- On the other hand, we said before that it doesn’t matter the order of the different branches, as we're looking at the structure of the tree, and it doesn't care who plays the matches. So we're talking about ‘strictly unordered binary trees’.

- We just have to use the internet browser, write 'how many strictly unordered binary trees can be formed', and wait for the results...

- Well, there aren’t many results. But I think none of them seems to fit what we're looking for. Perhaps we are not approaching the problem correctly.

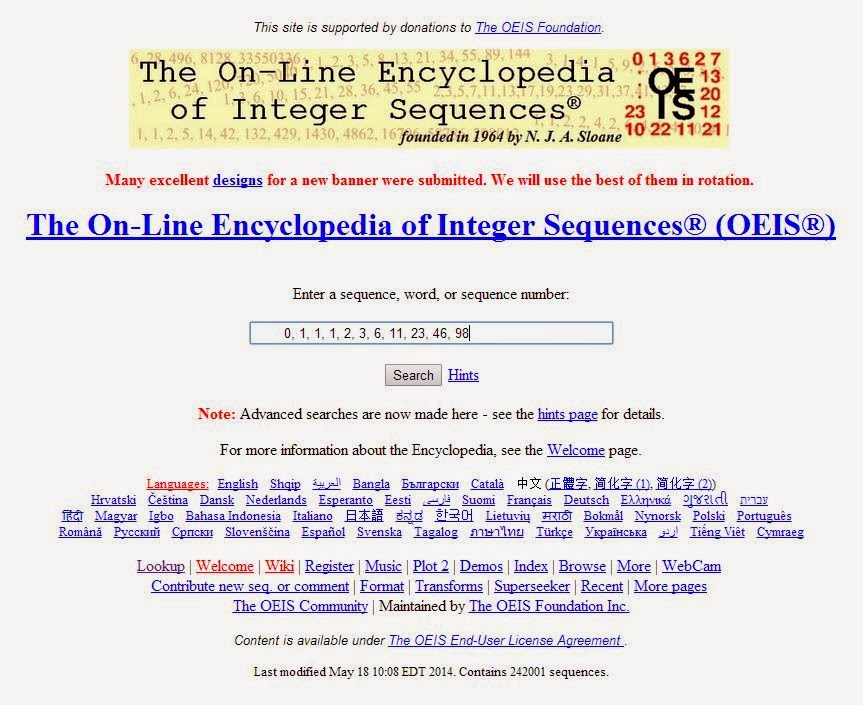
- Maybe it's better to resume again the series of trees that we had previously calculated:

0 1 1 1 2 3 6 11 23 46 98

- And we introduce it on this very useful website, which recognizes all kinds of series from its terms:

- Aha! Here we've got the solution: it’s series number A001190, called the Wedderburn-Etherington series. We can see that within the utilities described on the web, there’s the one concerned with our problem: the number of distinct ways of organizing a single-elimination tournament for n players (with the players name left blank), that's it, the amount of possible different schedules that can be set for a number n of participants.

- Now we just have to click the link where T. D. Noe calculates a table with the first 200 terms of the series, and pick the result for 61 teams:

844206159208807054529

- What a number! Let's put the commas, for to have an accurate idea of its magnitude.

844,206,159,208,807,054,529

- Over 844 trillion different trees! Even in the Amazon rainforest there aren’t so many trees!

- It looks like a pretty big number. And we said we wanted to study all the cases to see which system we adopt, right? I think we’ll have to work 24 hours a day.

- Well, let's think a bit. If one of us devotes 1 minute to each 'tree', and he/she doesn’t eat , sleep, nor rest, he/she needs a total of 160,617,610,995,447 years to finish the work.

- We should put to work on it all the Department.

- Nah, even if all Brazilians (over 201 million people), worked in this task it would take 7,989,625 years to complete it.

- Well, nowadays that almost everyone likes football, how about we ask the help of the entire world population?

- In that case, it would take only 221,987 years to study for 1 minute each of the possible ways of organizing our 61-teams tournament.

- By the way, I assume you remember when I mentioned that we weren't interested in differentiating the various teams, and therefore we focused only on the structure of the championship.

- Yes, but I didn’t quite understand why.

- Let’s revisit the issue for one moment. We have 61 teams, so we want to know the number of different ways we can sort them. In Mathematics, we talk about the permutations that can occur in a set of 61 elements.

- That’s right. And it’s easy to calculate. Any of the 61 national teams can be the first one to be chosen. For each one of them, we will pick another team among the remaining 60 teams. For each of these combinations of 2 teams, we have 59 teams to choose the third country. And so on.

- Therefore, the total number of permutations of the 61 countries will be:

61 · 60 · 59 · 58 · ..... · 3 · 2 ·1 = 61!

- Indeed, for brevity we use the expression 'factor of 61’, represented by the symbol of admiration. And if we calculate the product, we get the following result:

61! = 5.0758 · 10 ⁸³

- That’s a number five followed by 83 more figures. If you thought that the number of trees we saw before looked huge (8,4421 · 10 ²⁰), imagine how it will be this new number. And if we multiply the number of trees by the number of forms we can fit the 61 teams in them, we get a lovely number :

4.2850 · 10 ¹⁰⁴ = 42,850 · 10 ¹⁰⁰

- Forty-two thousand eight hundred and fifty googols of different ways of organizing our championship! We must remember that a googol is greater than the number of hydrogen atoms in the known universe...

- Uff . Then, I think we’d better use the traditional method: 29 matches of round of 64, freeing three countries in this first round, and full direct eliminatory rounds since round of 32.

- Brazil, and two others.

- Of course!

- Come on then! Let’s decide now which new countries we’re going to invite for completing the schedule of 61 teams. And we should think of organising something special for the opening ceremony: What about giving away some balls?

- Right. But first of all, if anyone is interested in this topic of tree structures, here you have some links to deepen on it: Tree (graph theory), Generation of Rooted Trees and Free Trees, Binary Tree.

- And here you have other links, if you liked the story and want to share it with your friends.

- Goodbye. And may the best win!

Si te gustó esta historia, puedes votar por ella en menéame y divoblogger. Muchas gracias. Si te gustó esta historia, puedes votar por ella en menéame y divoblogger. Muchas gracias.

Fibonacci also plays football

An interesting story that mixes football, mathematics, art, communications, sports bettings and nature, all around the Fibonacci sequence.

(This post participes on the xxxth edition of the Carnival de Mathematics, hosted by the blog Cuentos cuánticos.)

FIRST HALF

A new forward is coming. The board of Olympiacos F.C. (ΠΑΕ Ολυμπιακός) has decided to sign a new centre-forward, in order to strengthen the team for the next round of the Champions League.

The team owner, Evangelos, calls his friend, the editor of Protathlitis newspaper, to give him the scoop:

- Sotiris, we're signing a new striker. He’s a great Italian forward who plays in the Italian Serie B. Hardly anyone knows him, but he’s very good, plus we get him for little money. His name is 'Leo' (Leonardo).

- Can I get ahead of the news?

- No, please. In 30 minutes we’ll make a press conference to announce the new signing, and I don't want many people know the news in advance.

- So I can’t tell anyone? Let me inform my best friends by SMS. I promise you I won't spread it massively.

- Ok. I let you spread it, but with the following conditions: you may not send it massively. You can only send one message at a time. And you must tell this rule to the people you send the message, for them to do the same.

- Right, Evangelos, I’ll do it that way. But you haven’t told me the player's surname yet...

- You'll find out his surname if you look at the rules I've given you for spreading the message.

After hanging up, Sotiris, the Protathlitis daily director, sends the first message to the editor in chief, to be ready for editing the news just when the conference takes place, in these terms:

'A player named Leonardo will be the new Olympiacos FC forward. I don’t know his last name, but apparently it has to do with how this message is send. You can resend this message to your contacts, but only one at a time, please.'

After sending the message to the editor, the director sends a new SMS, this time to a friend, a fan of Olympiacos. And so he continues sending messages for 30 minutes before the conference starts.

Likewise, the editor, after reading the message, resends it to the layout designer, in order to prepare the front page. And within the next minutes, he goes on resending the message to other people, always one at a time.

And that’s what happens to the rest of recipients of the message.

We know that SMS sending is instantaneous, that everyone takes aproximately 1 minute to read the message, and 1 minute more to decide the person to whom will forward it. And we know that nobody has received the message from two different issuers.

With these data, and 30 minutes later, can you calculate how many people will know the news before the press conference starts? 100 people? 500? 1,000? And, most importantly, can you imagine what’s the second name of the Italian footballer?

SECOND HALF

I don’t know how to start with this problem...

So we best start from the beginning :-)

We will call ‘minute 0’ to the moment the owner of Olympiacos calls the newspaper director (person 1 = P1). There's nobody who already knows the news, that is, 0 people know the scoop (excluding the members of the board of the club).

In the first minute, they talk about the new player. So, at the end of the first minute, there's 1 person who knows the news.

During the second minute, the newspaper director decides that the first person who should know the news is the editor in chief (person 2 = P2). He writes the SMS message and sends it to him. So when 2 minutes have passed, there's still only 1 one person who knows the name of the footballer.

Now let's see what happens in the next minute. The director decides to send a new message, this time to his friend, the fan of Olympiacos (P3). Meanwhile, the editor in chief has read the message the director sent him. Now, there are 2 people who know about the signing, and there's one more person that has received the message, but has not read it.

In the fourth minute, the director sends a new message, this time to other friend (P4). The editor, once he has read the message, has resent it to the layout designer (P5). And the fan of Olympiacos has received the message from the director and has already read it. Now there're 3 people aware of the deal, and 2 more to which the message has reached them, but haven’t read it yet.

In the fifth minute, the director resends the message to another friend (P6). The editor does the same with a friend (P7). The fan of Olympiacos sends his first message, to P8. Meanwhile, P4 and P5 have read the message. Thus, we have 5 people who know the news.

In the sixth minute, that’s what happens: the director, the editor and the fan of Olympiacos send another new message (to P9, P10 and P11), P4 and P5 send their first messages (to P12 and P13), and P6, P7 and P8 read the message. Now there are 8 people in the know of the signingl.

In minute 7, the first five people send a new message. The next 3 make their first delivery. And the remaining five have just read the incoming message. Now there are 13 people who know the subject. And eight more will receive the message shortly.

We could go on until the 30th minute, but now we’ve got enough clues to figure out what's happening.

Yeah? Well, I just don’t see what happens... And with this rythm I don't think that many people will know the notice before the press conference starts

Wait a minute. Let's look at the number of people who know the name of the new player at the end of each minute:

0, 1, 1, 2, 3, 5, 8, 13...

I can't understand how these numbers are related to each other...

Try as follows: pick the first 2 numbers, add them up and tell me the result.

0 + 1 = 1

We’ve obtained the third number in the sequence. Now take the second and the third number, and add them up again.

1 + 1 = 2

Are we going to do the same with the third and fourth?

Yes, please.

1 + 2 = 3

I see how it works. Each number is obtained by adding the previous two, right?

That's right. In mathematical terms we’ll define it as follows:

F(n) = F(n-1) + F(n-2); F(0) = 0; F(1) = 1

This way, we’ll generate the following numbers until we reach number 30 in the series, which will be the one that indicates the number of people who knew the news before the press conference started.

Let's write down the numbers of the sequence, that mean the amount of people who know the news, and in brackets we'll write the corresponding minute:

0 (0), 1 (1), 1 (2), 2 (3), 3 (4), 5 (5), 8 (6), 13 (7), 21 (8), 34 (9), 55 (10), 89 (11), 144 (12), 233 (13), 377 (14), 610 (15), 987 (16), 1.597 (17), 2,584 (18), 4,181 (19), 6,765 (20), 10,946 (21), 17,711 (22), 28,657 (23), 46,368 (24), 75,025 (25), 121,393 (26), 196,418 (27), 317,811 (28), 514,229 (29), 832,040 (30)

Nearly a million people, in just 30 minutes, without performing mass messages!

Indeed, this sequence seems that progresses very slowly (in the first 10 minutes only 55 people know the news), but then it has an exponential behaviour.

In fact, if we continue with the series, and assuming that all inhabitants of the planet have mobile, and network coverage, the news will be known worldwide in just 49 minutes.

But if there are several people who send the message to the same person, this no longer fulfills...

That’s why, at the beginning of the story, we said that we knew that nobody has received the message from two different issuers. So we avoid that multiple people send the message to the same recipient. This doesn’t happen in real life, so the figures would be somewhat different from those calculated in theory.

In addition, we must consider another detail. Not all the people are interconnected. There may be 'islands' of people who will never receive the message. Imagine, for example, that all the Greek people have solely contacts of Greek people in their phones, and none from another country. The message would not leave Greece! Or think that people living in Oslo are all interconnected, but don’t have contacts of other persons outside the city. The message would spread throughout the world, except by Oslo.

Despite these drawbacks that can occur, it’s likely that, by the end of the press conference, almost everyone will already know the name of the new striker. However, the people who have guessed the surname of the player will be just a few.

And, what can be his surname?

You see, this sequence we've seen, in which each number is obtained by adding the two previous, is called Fibonacci sequence. Fibonacci was a mathematician of the 12th-13th centuries, significant because he introduced the use of Arabic numerals into Europe, and because he discovered, among other works, this succession when studying a problem about breeding of rabbits. However, this sequence was already noted by some Indian mathematicians some centuries before.

Then, the player is called Leonardo Fibonacci, right?

Actually his name was not Fibonacci. Fi-Bonacci means "son of Bonacci", which was how his father was known, an Italian tradesman. His real name was Leonardo Pisano (Leonardo of Pisa).

And by chance there’s an Italian striker whose name's: Leonardo Pisano. So, we have the full name of the forward!

Well, I had never heard about Fibonacci nor his series of numbers.

It's astounding, because it’s a sequence that appears in the most unexpected places, which leads to many mathematicians and laymen to engage in researching its characteristics and applications.

Among its properties, which would fill an entire encyclopedia, there are some really amazing.

For example, the square of each number in the series is equal to the product of the two adjacent numbers, adding or subtracting 1 (the difference alternates positive-negative-positive-negative -...)

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711...

144² = 20,736             89 x 233 = 20,737 = 144² + 1
233² = 54,289             144 x 377 = 54,288 = 233² - 1
377² = 142,129           233 x 610 = 142,130 = 377² + 1

Moreover, if we pick 4 successive Fibonacci numbers, we get that the difference of the squares of the two central numbers equals the product of the two extremes 

C²-B²=AxD.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711...

55²-34² = 1,869 = 21 x 89
2,584²-1,597² = 4,126,647 = 987 x 4,181

If instead of 4 consecutive numbers, we take 10 numbers and we add them together, we see that the sum is equal to the seventh number multiplied by 11.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711...

89+144+233+377+610+987+1,597+2,584+4,181+6,765 = 17,567 = 1,597 x 11

If you look at the latest figures from the Fibonacci numbers, we can see that every 60 numbers we find the same figures. If you look at the last 2 figures, they repeat every 300 numbers. The last 3 figures are repeated in 1500 numbers. And so on.

If we forget about the first 0, the third number is 2, and we find a multiple of 2 every 3 numbers. The fourth number is 3, and every 4 numbers we get a multiple of 3. The fifth number is 5, and every 5 numbers we find a multiple of 5. The sixth number is 8, and we have a multiple of 8 every 6 numbers. And so on.

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711...
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711...
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711,
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711,

The sum of all numbers up to a given one equals the number two positions farther, subtracting 1

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711..

0+1+1+2+3+5+8+13+21+34+55+89 = 232 = 233-1

And if we divide each number by the immediately preceding, we see that, as we move forward in succession, the result of this division is getting closer and closer to the value of the golden ratio, also known as golden section,  golden mean, golden number or Phi (φ).

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711...

1/1=1 2/1=2 3/2=1.5 5/3=1.666... 8/5=1.6 13/8=1.625 21/13=1.615... 34/21=1.619 55/34=1.617...

φ = 1.61803398874989484820458683...

This ‘golden ratio’ sounds me a lot. It's widely used in art, right?

Yes. Many artists used this ratio in their art works. Thus we have the Vitruvian Man, in which another Leonardo, da Vinci this time, draws a man starting from rectangles formed with the golden ratio. We observe the same on the Mona Lisa, or on the picture of the Last Supper. And other painters such as Michelangelo and Dürer also applied it widely in their works.

So this proportion has been used from the Renaissance...

No. It was known long before. Thus, we find it in the Athenian Parthenon (s. V BC), when analyzing the relationship between the parts, the roof and columns. And the Babylonian and Assyrian civilizations also used it.

So, it’s also applied to other various arts apart from of painting.

Yes, in addition to painting and sculpture, we can observe the golden ratio in the formal structure of many works of classical music of Mozart, Beethoven, Schubert, Béla Bartók and Debussy. And even in the arrangement of the shape of violins.

I see that this sequence has multiple mathematical and artistic applications.

And there’re more applications. We can find apps in other areas, truly amazing.

In nature, we can see how this series appears in the spiral arrangement of sunflower seeds. Thus there’re sunflowers containing 21 spirals in one direction and 34 in the other. And others have 55 and 89 spirals, or even 89 and 144, but always about consecutive Fibonacci numbers.

What a strange layout!

Well, it turns out that this is the best way on a circular flower to fit as many seeds as possible. We also find this layout in the pinecones with their double set of intersecting spirals: the total of right-turning and left-turning spirals correspond to the Fibonacci sequence: 5 and 8, or 8 and 13. Daisies group their seeds in 21 spirals in one direction and 34 in the other, and usually have 13, 21, 34, 55 or 89 petals.

If you look at the branches or leaves of plants, we see that they are always distributed so that they can receive the maximum sunlight and rainwater as possible. For this aim, its position around the stem or branch is determined by the Fibonacci sequence. And also occurs with roots, in order to cover the maximum possible terrain and therefore food, and so as to interfere as little as possible between them.

So the plant world is full of sequences of Fibonacci...

And also the animal world. For example, in human body, proportions between the distance from shoulder to fingers and the distance from elbow to the fingers, the height of the hip and knee, the joints of the hands and feet, or the height of being human and height of the belly button, among others, are determined by the golden ratio, so intimately linked to the Fibonacci numbers.

In the bees’ world, we find these numbers when we count the number of possible routes a bee can take by the hexagonal cells of a honeycomb.

We also find this pattern in how hares or rabbits multiply (that was the original problem in which Fibonacci stated this series) as well as other animals. And the DNA molecule measures 34 armstrongs long by 21 armstrongs wide!

There’s only left to find these numbers in the marine world...

Indeed. And for that, nothing better than looking at the shell of the Nautilus.

In it, each full convolution is at a distance from the center 1.618 (φ) times of the previous round. This spiral, called golden spiral (or Dürer spiral), can be roughly drawn by using the numbers of the Fibonacci sequence. And can be found in many animals as in the shells of snails or in the horns of ruminants, and even in the form of some galaxies.

In stock market, when a certain value has been going up or down for long periods, and changes its trend, the limit of the estimated variation or correction tends to correspond to the inverse of the golden number 1/φ= 61,8%. And Fibonacci numbers are widely used to identify changes in market trends, by setting time periods of 5, 8, 13 and 21 years in the graphic indices or values.

And can we find any application of these numbers in the world of football?

Not so much in football itself, but in something closely related to it: sports betting. For them, the Fibonacci system has been determined as one of the safest methods, especially when you bet on favorite..

It works as follows: the player will be making bets whose amount is determined by the numbers of the Fibonacci sequence. If you lose a bet, you should keep betting using the following number and amount of the sequence. And if you win, you must go back 2 numbers in the sequence, and bet that amount.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269...

This is a very good system for betting on favorite, as it’s very difficult to miss more than 5 consecutive times. The main drawback is that the growth rate of potential gains is a little slow, and for having big results you have to invest more time, but instead losses are minimized.

And these Fibonacci numbers have something to do with fractals, right?

Yes, they do. Do you remember the tables we have been drawing to see the evolution of the people who knew the news as the minutes passed? Well, we could have studied the evolution of the spreading of the news in a more graphically way.

We will assign a small circle to each person involved in the communication. We'll leave them blank when they don’t yet known the news because they haven’t yet read them, and we’ll paint them green one minute after receiving the news, because we assume that they have already read them.

We draw a blue arrow between two circles to indicate that a person is sending a message to another. We’ll paint a yellow line to show that the person is reading the message, and a red line to indicate that the person is thinking on the next receiver of the message.

And now look at our new scheme:

It’s clear that the layout of the scheme is a fractal: the main 'tree' (root in this case) repeats its form for any person you choose

It's true. Just one more question. To go getting the terms of the Fibonacci sequence, we have been adding the previous two. But would be there a formula to calculate a specific term of the sequence, i.e. the 49th term, without having to make all the previous sums?

Yes, of course. And guess who we find in the formula!

I’ve got no idea.

Our beloved ‘golden number’ o Phi (φ):

This is the formula :

ƒ_n = [(φⁿ-(1-φ)ⁿ]/√5

And if we apply this formula (attributed to Binet) to number 49, we get that, at minute 49 there will be 7,778,742,049 persons who would know the scoop.

It's clear that secrets are only secrets if you don’t tell them to anyone...

That 's true. In any case, this story is no secret, so you may spread it so widely as you want, even massively ;-) 

And if you're interested in learning more about Fibonacci, you can visit any of these wonderful links: Nature by numbers: the theory behind this movie, The Fibonacci sequence in nature, The Fibonacci numbers and golden section in nature, Nature, the golden ratio, and Fibonacci too..., Fibonacci in nature, Soccer betting system Fibonacci strategy, Fibonacci Numbers in Nature.

Si te gustó esta historia, puedes votar por ella en menéame y divoblogger. Muchas gracias.