(This post participates on the 119th edition of the Carnival de Mathematics, hosted by the blog White Group Mathematics.)
FIRST HALF

The coach of the Greenland's national team is very worried. Next weekend they play a decisive match to qualify for the Olympic Games in Rio de Janeiro, and she has a serious problem with the team's captain.
There's a tradition on the team of drawing lots to choose who should shoot the penalties, among all the players who want to do it.
The problem is that, for some time, all penalties have been kicked by the captain, and she has missed the last 10.
Pipaluk, the coach, has decided to call her friend Joe Vitruvius, to see if he helps her solve this mystery, and thus they can face the next match with the highest guarantees.
Joe answers the call of Pipaluk, and she goes to the Nuuk airport to welcome him.

- Hi Joe, I'm very happy you've come to help me.
- It's a pleasure. Tell me what's the problem.
- You better see it for yourself on the pitch. Let's come tomorrow to our training session.
- Ok, see you there.

On the following day, Joe goes to the stadium, and watches the curious way of choosing the player who will shoot the penalty.
- What's that what they do when they have to take a penalty? Why do they form a circle?
- That's the way they choose the penalty-taker: they do the puisi-nanoq game (the seal-bear game in Greenlandic).
- And what's that?
- All the players willing to take the penalty place themselves in a circle, and they're eliminated one by one as follows. They start counting from one of them, saying: puisi-nanoq-puisi-nanoq... (seal-bear-seal-bear...) And all the players who get a bear, are removed. The last ‘seal’ will be who kicks the penalty.
- How come?
- Yes, it's very simple, we play it since kindergarten. We start counting at one of them (we assign number 1 to her, so that this first player, which corresponds to a seal, stays in the circle, and the second one (bear) goes out. The third player (seal) also stays in the circle, and the fourth one (bear) is taken out. And we continue this way, eliminating one player of every two, and therfore the circle becomes smaller, till only one remains, who will be who will take the penalty.
- I can't see where's the problem. The 3 penalties have been kicked by different players. According to what I've seen, the number of players who want to shoot the penalty varies every time they have to kick one. Also, each time they stand in a different order when forming the circle, and they start counting from a different player.
- Yes, that's the way they do it on training sessions. But when playing official matches, the captain has the right of being the one who does the counting, and who decides from which player she will start from. And surprisingly, in the last 10 times she has always been the player selected to kick all the penalties.
- Yes, that's the way they do it on training sessions. But when playing official matches, the captain has the right of being the one who does the counting, and who decides from which player she will start from. And surprisingly, in the last 10 times she has always been the player selected to kick all the penalties.
- This wouldn't be a problem if she were a good penalty-taker. But she's the worst in this facet of the game, and we've already lost some matches for this cause. Next saturday we play to qualify for the Olympic Games, and I don't want take any risk. She says that she doesn't cheat, that she's very lucky. Is it really so, Joe?
SECOND HALF

- Just one question, Pipaluk: is the captain a Mathematician?
- No. She's got a degree on History from the University of Nuuk.
- Well, this would also explain her ability. I'm sure she knows the history of Flavius Josephus.
- Who's that?
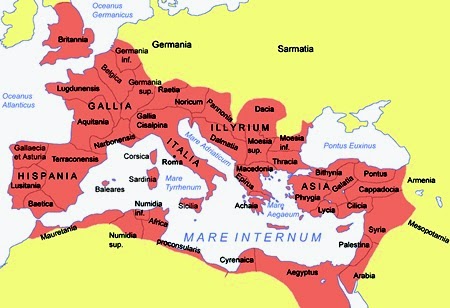
- Well, it's an old history, from the I century A.D., when Rome ruled all the Mediterranean Sea. The Jews had rebelled against the Empire, but the Roman army was very powerful.
- At the command of the Galilean troops was Flavius Josephus, who descended from a family of priests bound to the Israel kingdom. They were defending from the attack of the Roman legions at the impregnable fortress of Yodfat for some months, but they could no longer resist the Roman siege.

- When they realized that they would be captured, they decided to commit suicide rather than surrender dishonorably to the enemy. But Jewish law forbade them to suicide, so they adopted a curious process to carry out their purpose, which is known in Mathematics and Computing Science as the Josephus problem.
- The 41 Jewish soldiers still alive formed a circle, such as your players do. In their case, they counted in threes, so that the every third soldier was killed by his partner on the right. And they continued the procedure until Flavius Josephus was the last person alive, so he had to commit suicide, as they've agreed. But he didn't do so, but he gave himself to the Roman troops.

- He was sent to Rome as a slave of the imperial family Flavia, from which he took his name. Thanks to his academic education and his diplomatic skills, was finally released by the emperor Vespasian, and developed a broad work in Rome as historian and writer. Among his works, we can find the chronicle of this event that marked him for life.
- Some people think he saved his life by chance, or thanks to the Divine Providence, like he used to proclaim, but it seems clear that he knew where he had to stand to get rid of the fatal outcome.
- And that's exactly what happens to your captain. She's the one that points who's saved and who leaves the circle. So she firmly knows well how to be the player who kicks the penalty.
- Yes, but she's the first player to place herself in the circle. She doesn't know how the other players are going to stand in it, nor how many will be.
- Yes, but she's the first player to place herself in the circle. She doesn't know how the other players are going to stand in it, nor how many will be.
- That's true, but she's who decides which player she starts from. And there's the trick. She knows the correct position to stand in relation to the first player, so to be the last to go.
- Ah! And how?
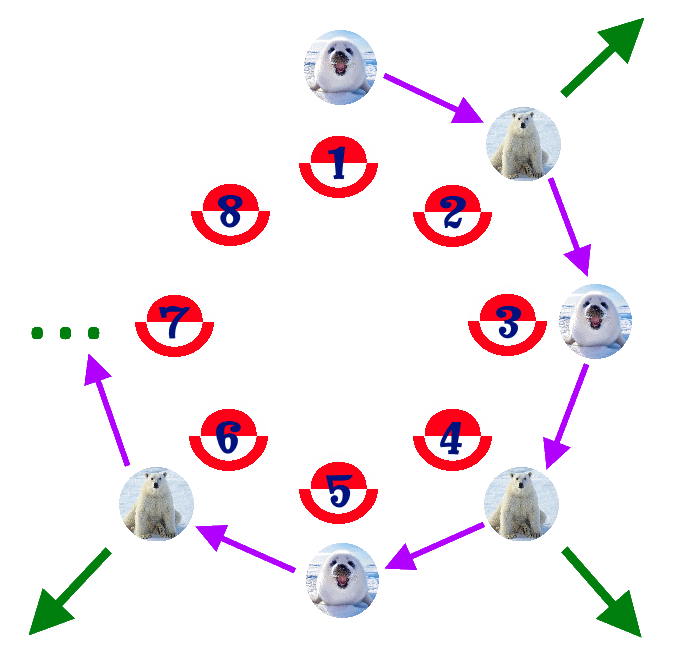
- I'll explain it to you with an example of a group of 6 players. We're going to number them, beginning by the top, and following clockwise.
- And now we go ahead and play your seal-bear game. We start from player number 1, who's assigned a seal. We tag player number 2 as a bear and we remove her. Number 3 gets a seal, and 4 is named a bear and is counted out too.
- Now there are only 4 players left in the circle. We follow on with number 5 (seal), who saves, and we take out number 6 (bear). We keep on going around the circle, so that number 1 gets again a seal. Number 3 is a bear, so we eliminate her. Number 5 is a seal and stays, and now number 1 is a bear and goes out. It will be number 5 who will kick the penalty.
- We know that, with 6 players, the choice will be number 5. If we follow this procedure with different amounts of players, we get the following results:
- Now I understand, the captain has learnt all this sequence of numbers, to know where she has to place herself depending on how many of players form the circle, right?
- Maybe, but it's not necessary to learn them. We can find a formula.
- And how would it be?
- If we look at the table, we see that when the number of players is a power of 2 (1, 2, 4, 8, 16, 32), the player number 1, from which we start to count, is the winner player.


- Yes, it's true.
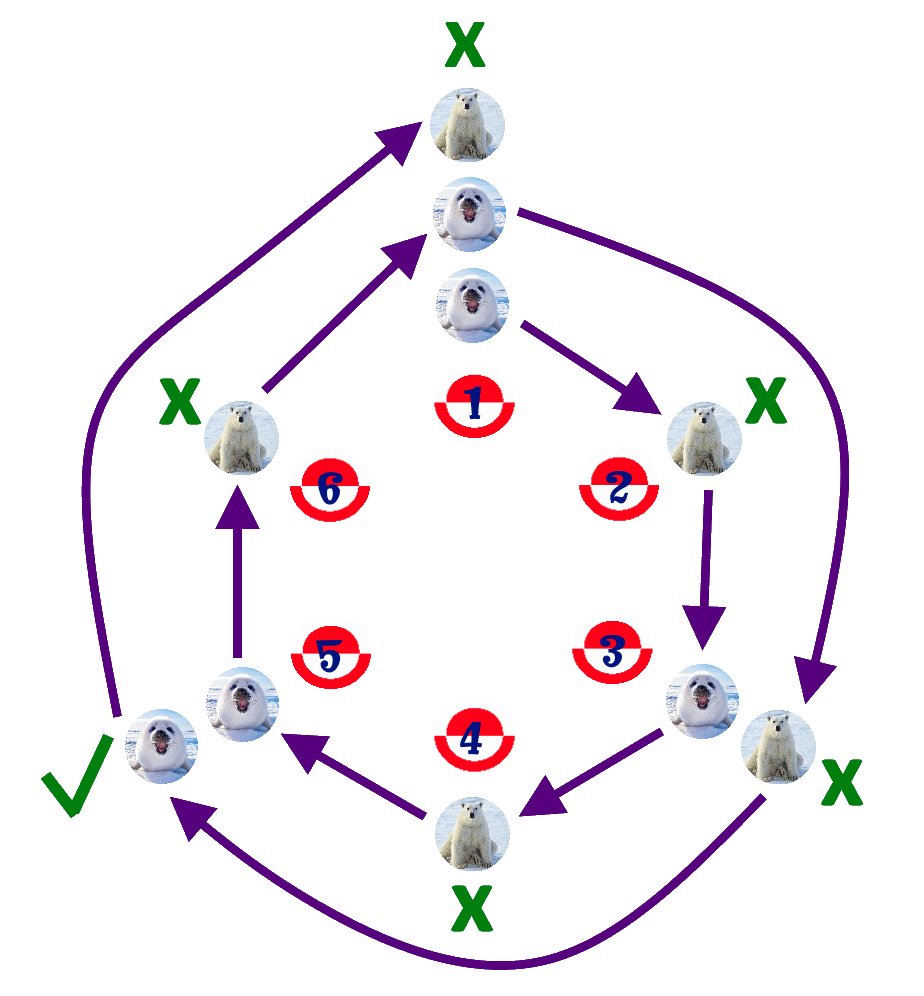
- It's easy to understand if we study it a little. Imagine we've got 16 players (16 is a power of 2: 24 = 16).
- In the first round to the circle, all the players occupying even positions will be eliminated, and we'll have half of the initial players.


- We go on with the game, and all the players occupying even positions get removed again in the second lap.


- We do the third round to the circle, and number 1 avoids the elimination once more. And finally, when there are only 2 players left (number 1 and number 9), the second one is also removed. So number 1 is saved in all the laps. And this will always happen when the amount of players is a power of 2, because after each pass there's always an even number of players.


- Yes, but what can we do when the number of participants is not a power of 2?
- Then we must be skillful enough to calculate how many players have to go out till we have a number of players that is a power of 2, so that in this moment we'll be in the position that would be number 1 of the new circle formed after eliminating the last of the players who exceed the power of 2.
- What did you say?
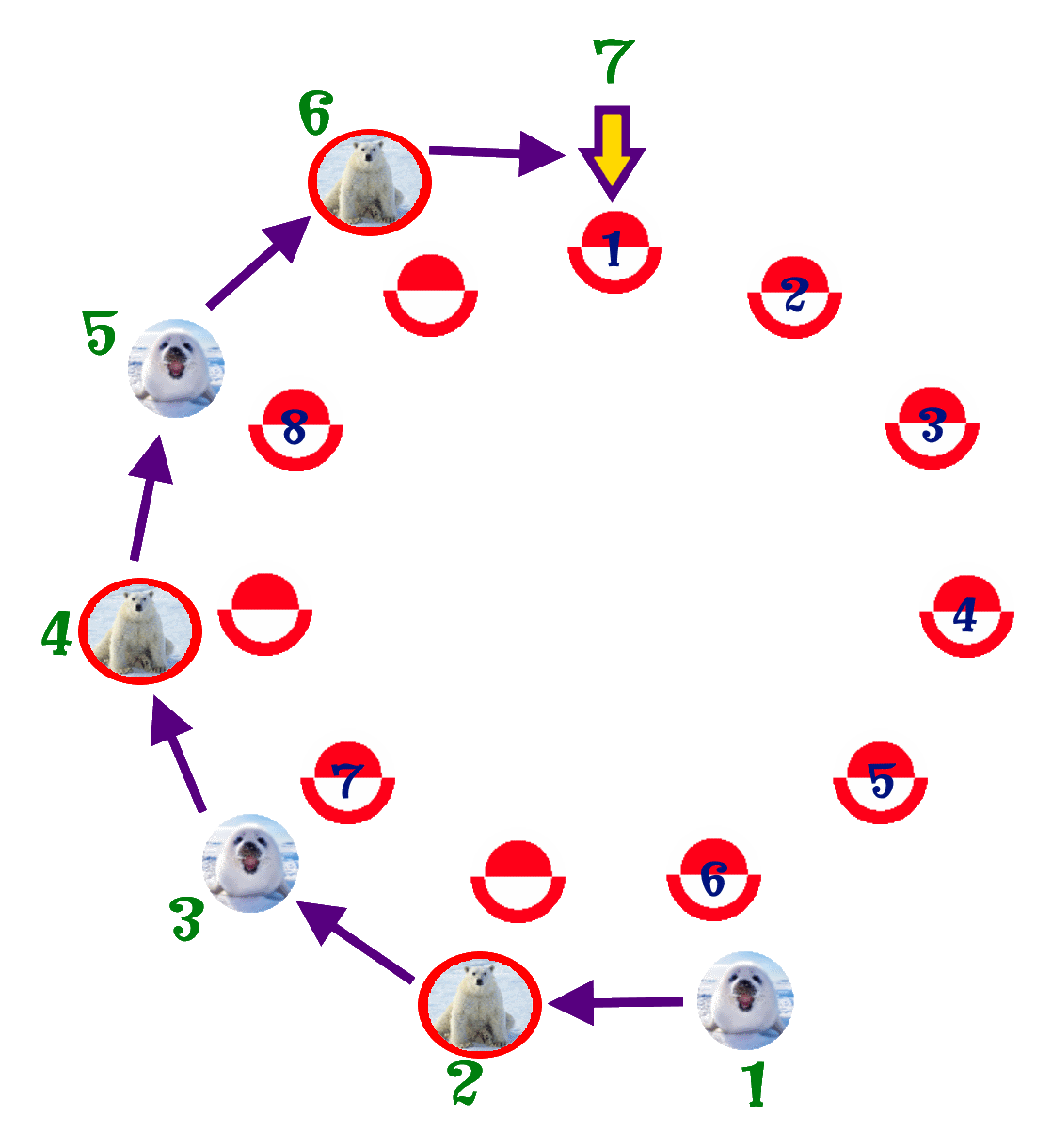
- Suppose that we have 11 players instead of 8. We must achieve to be in position number 1 when we're only 8, so we can apply the method we've seen before, since 8 is power of 2 (23 = 8).
- So we have to count 3 'bears' backwards from our position. And so we get to place ourselves in position number 7, so that we'll be number 1 of the new circle of 8 players formed after we take out the first 3 players in the group of 11.
- If we want to generalize the procedure, we have to think on the total number of players, which we'll call n (in our case 11). Then we'll calculate how much (k) exceeds this number the previous power of 2:
k = n - 2m, where m is a positive natural number such that 2m < n < 2m+1
(in our example k = 11 - 23 = 3, with 23 < 11 < 24)
- And our optimal position (p) in the circle is given by the formula:
p = 2 · k + 1
(in our case p = 2 · 3 + 1 = 7)
(in our case p = 2 · 3 + 1 = 7)
- And that's what your captain does. She places herself on the seventh position of the circle, that is, she starts counting at the seventh player on her right.
- And don't you know an easier way to calculate it?
- Yes, if you know well the binary system. You just have to convert the number of people within the circle into binary. Then you transfer the first 'one' to the last place ot the binary number, and you re-convert the resulting number to the decimal system. And so we get the place where you have to stand for being the winner.
- For example, for 21 people, the optimal place is the eleventh, as you can see:
- Yes, if you know well the binary system. You just have to convert the number of people within the circle into binary. Then you transfer the first 'one' to the last place ot the binary number, and you re-convert the resulting number to the decimal system. And so we get the place where you have to stand for being the winner.
- For example, for 21 people, the optimal place is the eleventh, as you can see:
- I understand. And, how could we avoid this? What if, instead of eliminating every second player, they make it with a step of three (seal-seal-bear-seal-seal-bear...), or with any other number?
- It'll be the same, although with higher numbers its calculation becomes more difficult. With a computer, we can find the solution in several websites like this or this other.
- And it's useless to entrust this task to another player, because sooner or later she will learn the algorithm.
- So one solution is to change the system of choice. You should choose the player who has the best statistics on penalty shots, although this may generate some problems, as happened in the story And now, who kicks the penalty?
- No, never. The seal-bear game is an old tradition in our land.
- I can think on other solution. Listen:
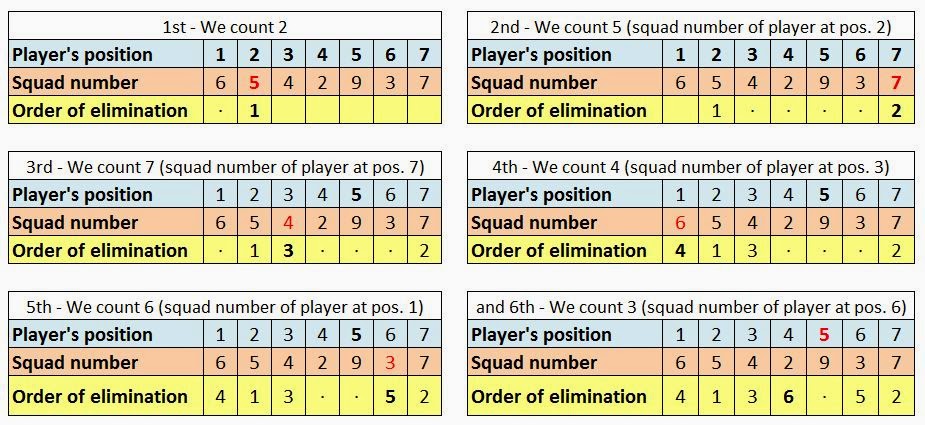
- After doing the first couple seal-bear, so that the captain can eliminate the worst penalty-taker, then she'll look at the number on the player's back, and use this number to reach the next ‘bear’ to be removed. Thus, if it's a 5, she'll sing 'seal-seal-seal-seal-bear'.
- If the next excluded player wears a 7, she'll count 6 seals and 1 bear, and so on. That way it will be almost impossible to figure out who will be the last survivor, although the game is determined from the first choice.
- But, what if she's able to calculate mentally and quickly who'll be the last one, because she knows the squad numbers of all her playmates?
- Even though, it will be impossible in many cases to find a winning combination that allows us to be always the last one.
- Suppose, for example, that we put on the circle the players with shirt numbers 5, 6, 7, 8 and 9, in this order, and that the captain has number 5, let's see what would happen to our game with our new rules we've set.


- We can check that the last winner depends on who's removed first, but in neither case players 5 and 7 will be the last 'seals', and on the contrary, players 6 and 9 will be more likely to be the winners.
- Well I like this variant you've invented. I'm sure that we'll finally prevent the captain kicks all the penalties, and we will qualify for the Olympic Games. Thank you very much for you help, Joe.
- I'm sure you will succeed, Pipaluk. Good luck for the match!

If you're interested in learning more about this topic, you can visit any of this wonderful articles: Formulating the extended Josephus Problem, On the Josephus problem, Josephus problem, Josephus Flavius Problem: Recursive Solution, Powers of two in the Josephus problem The Josephus problem.
Below this lines you will find other links, for if you liked this story and you want to share it with your friends.
Don't forget to take a walk by the Carnival of Mathematics. There you'll find lots of excellent math posts that you'll surely like too.
Also, if you think of any other way to play the puisi-nanoq game in which the captain can't choose in advance who will win, you can share your idea by writing a comment below.
Also, if you think of any other way to play the puisi-nanoq game in which the captain can't choose in advance who will win, you can share your idea by writing a comment below.
















No comments :
Post a Comment