The mathematical language is so amazing that, with a few figures, and a pair of operations, we can create formidable numbers.
(This post participates on the 121th edition of the Carnival de Mathematics, hosted by the blog Life through a mathematician's eyes.)
FIRST HALF

The players of Los Angeles Galaxy team are very happy. They've just won the Major League Soccer Cup.
Once the celebrations for the victory have finished, president Chris Klein has promised them an economical reward for their victory:
- I've come to the changing room to tell you our decision of giving you a gift for your success.
We're going to give you as many cents of dollar as the greatest number you may be able to form with three of your shirts (you can't use those with double figures, nor use the number zero or the infinity symbol, right?).
- For example, if you put togheter the shirts with numbers 5, 2 and 7, we'll give you 527 cents of dollar.
- For everyone?
- Oh, no! Our budget is not so big. It will be 5.27 dollars for all the team. You can share the amount the way you decide.
- Can we repeat numbers?
- No, you can't use three shirts of the same player.
- And can use mathematical symbols?
- Ok, you can, as long as you don't repeat them. And if you use one symbol, you must remove one number.
- That is, if you use, for example, the plus sign, then you must remove one figure, so you can use only two digits: 5 + 9.
- So for every sign we use, we must use one digit less, right?
- Right.
- And when should we tell you the answer?
- Tomorrow morning. The wishes of the club are that you can enjoy your well deserved reward as soon as possible...
- All right. We see you tomorrow.
The players will meet in the evening, after the training session, to see what amount they will ask the club.
In addition, they've called Joe Vitruvius, who is on holiday by the West coast, to help them with this problem.
SECOND HALF

The sun starts to fall down, and the football players met on the top floor of a skycraper in the city of Los Angeles.
- Well, let's see what we can do.
- I see that, if we're going to use only numbers, it's clear that the highest number is 987. So we'll get 987 cents, that is, 9.87 dollars. A high fortune, to be shared between all of us!
- Yes. And if we use some mathematical symbols, it seems that we'll only lose money.
- We can leave apart the subtraction sign. If we use it, we'll also lose money. The best option, without using the zero, would be 9 - 1 = 8 cents.
- The sign of addition doesn't seem to be very helpful. From our chosen number, if we replace any of the digits with this sign, we certainly lose a lot of money again. At best, we'll get 9 + 8 = 17 cents, far from the initial 987.
- And with the multiplication symbol (here we'll use a dot) we can't either improve our prize. In this case, among all the possible products, the most beneficial one would be 9·8 = 72 cents. Still far from the 987 cents.
- And with the multiplication symbol (here we'll use a dot) we can't either improve our prize. In this case, among all the possible products, the most beneficial one would be 9·8 = 72 cents. Still far from the 987 cents.
- Obviously, if we introduce the division symbol, we won't achieve anything positive, not to mention the square root...
 - Don't think more about it, We'll ask 987 cents, and problem solved!
- Don't think more about it, We'll ask 987 cents, and problem solved!
- Do you agree with us, Joe? You've been very quiet, during our discussions...
- Oh, I haven't said anything because all your arguments were right. All, except the final decision you've taken.
- Why?
- I think you've forgotten a very useful mathematical operator: the exponentiation. It's a particular case of product in which one of the numbers (the exponent) shows how many times we have to multiply the other number (the base) by itself.
Thus, we have for example 93, which means 9·9·9 = 729.
All we have to do is to place some numbers at a higher level from the others, and that's all.
Althought it has not always been like this. Babylonians, Greeks (especially Diophantus), Arabs, or medieval mathematicians used different symbols and words to describe the squares, the cubes, and the rest powers of a number.
Michael Stifel, in his ‘Integra Arithmetica’ of 1544 introduced the concept of exponent. James Hume, in 1636, decided to set the exponent on a higher level in relation to the base, although he used Roman numbers to designate them. And finally Descartes, in his work ‘Géométrie’ replaced the uncomfortable Roman numerals for the Hindu-Arabic numbers.
So, thanks to Descartes, this operation will be free for us, because we don't have to use any extra character so we don't have to eliminate one of the figures. Now, our problem is how to place the digits in the most favourable order.
As you can see, I've eliminated some combinations. For example, we know that 897 has to be smaller than 987, so we don't calculate it.
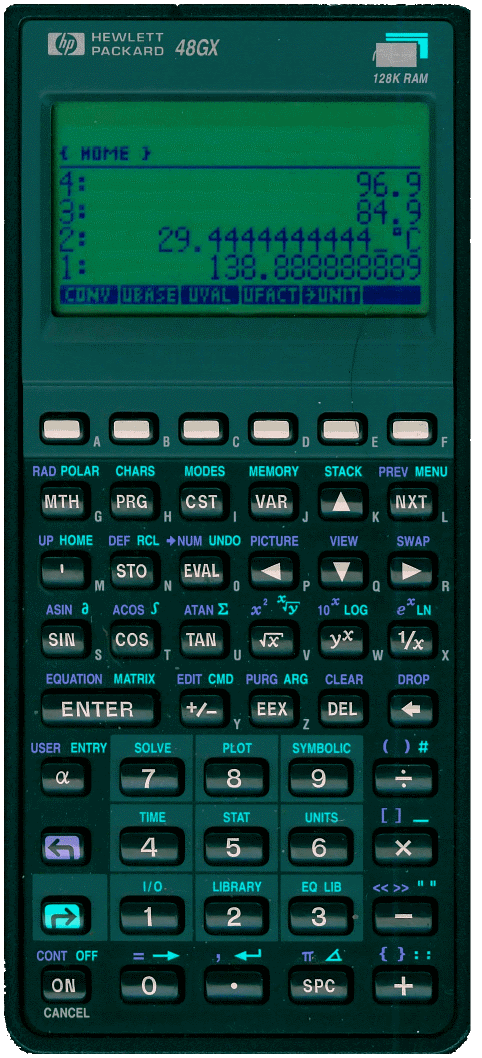
- Joe, I've got a scientific calculator in my backpack.
- Yes, and I downloaded a calculator app for my mobile. We could use it.
- I'm afraid that none of them will be useful for our purpose. Both apps will get blocked with the operations.
In fact, there are lots of internet websites that offer services of calculation for huge numbers, and they wouldn't be able to make these calculations. But there's a powerful one. This is the HyperCalc JavaScript website. We'll use it for getting the results of the various options.
Now we're going for the last row of my table of possible combinations: 987, 978, 897, 879, 798and 789. In this case, each combination of numbers can be calculated by 2 different ways. If we take number 987, we can calculate first 98 and raise the result to 7, or we can calculate first 87 and then take number 9 and raise it to the result we got.
Let's see the results:
 - According to this, we get the highest number with the combination 7(89). So we'll ask the club 789 dollars.
- According to this, we get the highest number with the combination 7(89). So we'll ask the club 789 dollars.- Great! We can now go home!
- Don't hurry, strangers! There's still something to be done.
- What do you mean?
- Well, I think that you're fogetting another mathematical symbol.
- Ah, yes? I can't think of anything.
- Well. There's a symbol that will cause admiration to some of you... It's the sign:
- Is it a mathematical sign, too? And what is it for?
- This symbol represents the factorial function of a number. The factorials consist of the product of all positive integers from 1 to the related number.
That way, the factorial of 5, written 5!, will be the product of the first five integer numbers:
5! = 1·2·3·4·5 = 120
And the factorial of 9 will be:
9! = 1·2·3·4·5·6·7·8·9 = 362,880
- We know when to use the signs of addition or multiplication. But, when can we use these factorials?
- They've been used for a long time, especially in Combinatorics and in Mathematical Analysis. Hindu Mathematicians used them yet in the twelfth century. And they're used, for instance, to calculate the number of different ways of arranging some distinct objects.
For example, if we want to know how many differents forms you can enter the pitch (the 11 players going one by one, not by pairs, and assuming that the starting lineup is always the same), we get a total of:
11! = 1·2·3·4·5·6·7·8·9·10·11 = 39,916,800 different ways of entering the pitch.
I mean that, if you play a match every 2 hours, 24 hours a day without resting, you could be over 4,556 years playing football without repeating the entry order to the field.
- Blow it!
- And why are factorials represented by the exclamation mark?
- Well, the first person who used this symbol was Christian Kramp in 1808. He was a Math teacher at Strasburg, who made a in-depth study on factorials. Initially he used a symbol in the form of a right angle, placed on the lower right corner of the number.
But he had problems with the printer's, so for the edition of his book Elements d'arithmétique universelle, he decided to use the exclamation mark just after the number.
What I ignore is why he chose this sign, used to express happiness. The symbol comes from the Latin word iocundum, which means happy, pleasant, nice. First it was shortened to the expression (io), that became an expression of happiness, and then the capital 'I 'was placed over the small 'o', and that's how this symbol was born, as a sign of exclamation.
Maybe the relationship between the symbol and the factorial function is the wonder caused in people when calculating the result of the operation. Just look at what happens when we change one of our digits, i.e. number 7, by an exclamation mark:
98! = 9.4268 · 10153
That is, a 154-digits number!
- Yes, it's a huge number. But I remember that with potences we got a higher amount:
789 = 7,3785 · 10113,427,138 > 98! = 9,4268 · 10153
- Then it seems quite clear: we get 789 cents. Or do you have one more surprise for us, Joe?
- Yes, we can still mix both operations to try to get the highest number.
If we want to observe the imposed conditions, it seems that there are six possible combinations. But it's very difficult to choose one of them.
I don't know what's better: to put the highest digit as the base or as the coeficient:
23 (8) < 32 (9) but 34 (81) > 43 (64)
And I don't know where to place the factorial symbol, after the base or after the exponent:
2!3 (8) < 23! (64) but 3!2 (36) > 32! (9)
We'll have to use again the HyperCalc JavaScript website and get the different results:
- I think that we finally will choose the option of 89! better than 789
- It seems a great amount of cents, but I'm sure it won't be a problem for Los Angeles Galaxy, right?
89! = 1,7828 · 101.032.606.169 > 789 = 7,3785 · 10113.427.138
- It seems a great amount of cents, but I'm sure it won't be a problem for Los Angeles Galaxy, right?
- I'm afraid this is going to be a problem. Are you aware of what this number means?
- Hmmm…
- It's a number of over 1,032 billion digits.
- It's not very big, isn't it?
- Do you know how many atoms are there in the universe? About 1087, that is, a number 1 followed by 88 zeros.
- Well, I can't see much difference between both numbers. Just a few more digits in the exponent.
- With scientific notations it's quite difficult to be conscious of the magnitude and the proportion of numbers. To get started on this subject, there's a great website that explains it very well: The scale of the universe.
Look: the volume of an electron is estimated to be 9.36·10−44 m3, and the volume of the universe is about 7·1081 m3. Well, if we fill the whole universe with electrons, the amount of these would be of 7.4786 · 10124. This will be as long as we leave no space between them, and we know this is not possible because of the laws of sphere packing.
Now let's imagine that all the universe, full of electrons, was compressed to the size of an electron, and we fill up again another universe like ours with those little universes full of electrons.
And imagine we repeat this process 8 million times. The final universe, full of small universes, full of small universes, full of small universes….(8 million times)… full of small universes full of electrons would contain as many electrons as the cents the club should give us.
- That way, it does seem a very high amount. Perhaps we'd better choose another combination of numbers to get an amount that the club can afford…
- All the money in circulation worldwide is estimated to be about 80 trillion dollars (80·1012 $). So there you have the upper limit of your request.
And you also know which is the lower limit: when I was entering in the skyscraper, I saw lots of young fans at the main entrance because they knew you've met here, and have begged me to ask if you can sign some autographs for them.
- Yes, perhaps we'd better forget those big numbers, because we already have got enough reward with the smile of these supporters. I think that our satisfaction and the children's can be also calculated with a potence, don't you think so, Joe?
- Let's go down immediately!
- Let's go down immediately!

If you're interested in learning more about this topic, you can visit any of this wonderful articles: The History of Mathematical Symbols, History of Mathematical Notation, The origins and development of mathematical notation, The History of Exponents.
Below this lines you will find other links, for if you liked this story and you want to share it with your friends.
Don't forget to take a walk by the 121th Carnival of Mathematics. There you'll find lots of excellent math posts that you'll surely like too.



















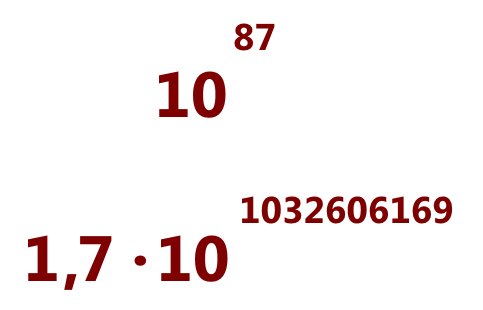


No comments :
Post a Comment