Sometimes it's quite difficult to get a truthful answer from people in surveys. Fortunately, some mathematical methods have been created to overcome the reluctance of people to answer some awkward questions.
(This post participates on the 123th edition of the Carnival de Mathematics, hosted by the blog Mathematical mystery tour.)
FIRST HALF
Next week there's an interesting semifinal of the AFC 2015 Champions League between the Chinese Guangzhou Evergrande and the Korean Kashiwa Reysol.
Fabio Cannavaro, coach of the Chinese club, has noticed that, in the last weeks, the level of play of his team has dropped a lot.
Some people say that some players of Guangzhou go out partying at night, and that's why they don't perform well in training sessions and matches. But nobody has proved it's true.
The club has hired some private investigators to follow them, but for now the players have always got rid of the detectives' persecution.
Fabio is worried about it, and doesn't know what to do. He has called them one by one to his office, and has directly asked each one if rumours are true. But none of them has accepted that goes out at night. And they didn't want to say how many colleagues use to do it.

It seems clear that they have lied, and that they form a very close group, and that they don't want to betray each other. But Fabio needs to know whether the problem of the trips at night is widespread or not among the team.
Tonight, while dinning at a restaurant in Hong Kong, he has met Joe Vitruvius, who has come to the city to take part in a Conference of Mathematics. Fabio has commented him on his problem, and Joe thinks that he should call his players again to his office.

- But they will answer the same again, Joe.
- Not necessarily. You can get some of them to tell the truth.
- Well, I don't see how. I don't want to threaten them, nor to offer them any kind of reward to betray their teammates.
- Well, there's a way to get them to tell the truth, without threaten nor rewarding them...
Can you imagine how they will know what's happening with the players?
SECOND HALF

- Let's see, Fabio, which were the questions you did?
- First, I asked: Do you go out for party at night? And everyone told me 'no'.
And then I asked: Do you know how many playmates like partying all night? And they answered me that none.
- Well, I think you should call them back one at a time and ask them the same questions.
- I don't understand, Joe. If I ask them the same questions, I will get the same answers.
- I've already told you that you won't be able to bribe them. And even less with a simple coin, no matter how pretty or magical it is.
- I'm sure this coin will help us to know the truth, Fabio.
- I can't see how.
- It's very simple. We'll call them one by one to your office, and we'll propose this: we'll give them this coin, and we'll tell them to toss it secretly.
If they get a panda bear, they must answer truthfully about whether if they go out on a spree or not.
But if they get the snake, they always have to answer that they do go out at night, regardless of the truth.
But if they get the snake, they always have to answer that they do go out at night, regardless of the truth.
They'll flip the coin again. If they get a panda, they must tell us the number of players they know going out by night, while if they get a snake, they can invent the amount, and tell any figure between 0 and 20.
We will never know, anyway, if each individual player has got a panda or a snake, that is, we won't know if he's lying or not, so those who has got a panda will have no fear of telling us the truth. Do you think they will accept this deal?
- I think so. It seems that the method doesn't compromise them.
- Here we go. Tell the first player to come in...
- ...we've finally completed the survey, Joe!
- Well, now we can get a clear idea about what's happening on your team.
- Well, now we can get a clear idea about what's happening on your team.
- Oh, yes? You'll have to explain it to me. We don't know if each player has lied or has answered truthfully.
- Let's see the results of our survey. Regarding the first question, in which we directly asked if they go out or not, we have a total of 12 positive answers and 8 negative ones.
We have a 50-50 chance of getting a panda or a snake, so the most likely is that half of the players have told the truth and half the players have lied.
This means that, about 10 players have said that they go partying at night because they have got the snake. And among the other 10 players who got the panda, and therefore had to say the truth, 2 have answered that they go out, and 8 have answered that they don't.
They are 2 from 10, that's it, a 20% probability, so in the total of 20 players of your squad, we could think that there will be only 4 players go on a spree at night.
They are 2 from 10, that's it, a 20% probability, so in the total of 20 players of your squad, we could think that there will be only 4 players go on a spree at night.
- Yes, but if it happens to get 20 pandas by chance, then all the answers would be true, and I'd have a problem with 12 players.
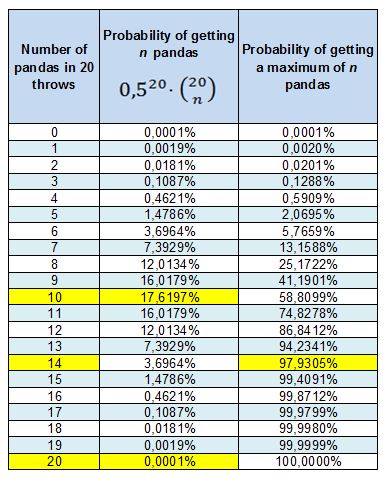 - It's true. But look at this other table. If we calculate the probability of getting a certain number of pandas, when we toss a coin 20 times, we can see that, first, the most likely option is that we get 10 pandas, a 17.62% of the times.
- It's true. But look at this other table. If we calculate the probability of getting a certain number of pandas, when we toss a coin 20 times, we can see that, first, the most likely option is that we get 10 pandas, a 17.62% of the times.
And, on second place, we notice that the chance of getting 20 pandas is about a 0.0001%, that is, once every million times we do the test. In fact, there is a probability of almost 98% that we get 14 pandas at maximum.
By the way, it seems a little risky to draw conclussions from a sample of only 10 players. So we should analyze the answers to the second question, in order to check if our assumptions are correct.
 - But here, Joe, we find the same problem. We don't know which data are true and which data are invented. In fact, we have a set of answers, quite diverse. Some have answered that no player goes out, and other have said that there are 20 revellers.
- But here, Joe, we find the same problem. We don't know which data are true and which data are invented. In fact, we have a set of answers, quite diverse. Some have answered that no player goes out, and other have said that there are 20 revellers.
- We can work on it, Fabio. If we calculate the average of the answers we have, we get that 5.25 people like partying. But the coefficient of variation, which measures the data dispersion, is enormous. We should work hard with sample data to obtain more acceptable statistical values.
We know that about half of the responses are invented, and therefore only half of the data are reliable. So we should try to eliminate some data, to get a more realistic average.
- But, how can we separate right data from invented data? If the second answers were related to the first responses, we would know that the data from those who said that they don't go out are correct, but they tossed the coin again before answering the second questions, so we can't get any help from this point.
- But, how can we separate right data from invented data? If the second answers were related to the first responses, we would know that the data from those who said that they don't go out are correct, but they tossed the coin again before answering the second questions, so we can't get any help from this point.
- That's true. I've made them flip the coin twice just in order to avoid they lie when answering the second question for those who have answered truthfully the first one and have answered that they don't party late at night, because therefore we know that they got the panda and are obliged to tell the truth.
Fortunately, in Statistics there are some methods to eliminate invalid data that can distort the average.
Fortunately, in Statistics there are some methods to eliminate invalid data that can distort the average.
Some statisticians remove those values furthest from the average 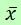 , distanced from it by a certain multiple of the standard deviation
, distanced from it by a certain multiple of the standard deviation  , and keep only the data in the interval
, and keep only the data in the interval 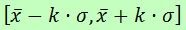 .
.
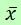 , distanced from it by a certain multiple of the standard deviation
, distanced from it by a certain multiple of the standard deviation  , and keep only the data in the interval
, and keep only the data in the interval
In other cases, we can sort the data from the lowest to the highest, and remove the first and the fourth quartile, leaving only the data of the two central quartiles, closer to the median.
With either of these two options, we can see how the standard deviation drops down considerably to a somewhat more acceptable value.
With either of these two options, we can see how the standard deviation drops down considerably to a somewhat more acceptable value.
Although in our case, as we only have 20 data, we must be cautious when removing some of them. By the way, we have 3 values that we can reject because they're impossible.
- And, which are they?
- And, which are they?
- If there are 8 people who say that they don't go out, it's impossible that there are 17 or 20 lively players. And there's no way that 0 players go partying because, in that case, all the players who have got the panda should have answered that they don't know anyone who goes out, and there should be several zeros, not only one, except in the very unlikely event that they got 20 snakes.
- Yes, once in a million times that we did the survey, right?
- Yes, once in a million times that we did the survey, right?
 - OK. We could go on the process by eliminating those less likely results, the furthest from the median or the average. Even in that case we could get confused, because not all the players know what they playmates do at night.
- OK. We could go on the process by eliminating those less likely results, the furthest from the median or the average. Even in that case we could get confused, because not all the players know what they playmates do at night.
You know that not all of them are friends of each other, and that they don't have fun all together. That way, if we eliminate, for example, the datum of 2, maybe this number has been provided by a person who was telling the truth, but it's also incorrect, because he only knows 2 people who do it, but there are much more.
As the sample we have is very small, perhaps the bias that we generate when performing a screening of the remaining data would be more prejudicial than beneficial, so we will simply make the average of the data we have so far.
- Then, at the end, which of the methods of data cleaning will be use?
- If we eliminate some data, we can see that the method with a lowest coefficient of variation is that of the central quartiles. Anyway, the average of all the methods is close to the value of 4. And this figure coincides with the result of the first question, so we can conclude that around 20% of your players goes out at night.
- If we eliminate some data, we can see that the method with a lowest coefficient of variation is that of the central quartiles. Anyway, the average of all the methods is close to the value of 4. And this figure coincides with the result of the first question, so we can conclude that around 20% of your players goes out at night.
Therefore, you can be happy, Fabio. It's very likely that only 4 players like to go for partying!
- That's right, and this means that the poor performance can be combated with more physical and tactical sessions. Now, the last work is to convince the 4 merry players to control themselves until we have won the championship...
And, are you sure that this method we have employed is reliable?
- Of course. This ingenious method is attributed to Eduardo Cattani, an Argentinian professor of Mathematics and Statistics at the University of Massachusetts, as Adrián Paenza refers in his book “Matemática... ¿estás ahí?". Morevoer, Stanley L. Warner, an American mathematician, published in March of 1965 an article about randomized responses and survey techniques for eliminating evasive answer bias in the Journal of the American Statistical Association.
Clearly, there are certain questions on sensible iussues like drugs consumption, sexual behaviour, illegal or forbidden topics, violence, bullying, socially frowned conducts, etc., in which respondents use to reply with incorrect answers.
 The one way to ensure the anonymity and the privacy, and therefore to win the confidence of the respondents, is using these techniques of randomized answers, although they don't always work, sometimes because respondents just don't understand the mechanism, sometimes because they don't trust in all the procedure, and sometimes because, despite everything, they don't respond truthfully.
The one way to ensure the anonymity and the privacy, and therefore to win the confidence of the respondents, is using these techniques of randomized answers, although they don't always work, sometimes because respondents just don't understand the mechanism, sometimes because they don't trust in all the procedure, and sometimes because, despite everything, they don't respond truthfully.In our case, as we have done two questions on the same matter, we can be more sure of the result of our enquiry.
- Great, Joe. Many thanks for all. Have a good time in China!
- Sure, Now, I go for a walk through the center of Guangzhou (Canton) to see if I meet any of my Chinese
friends
or perhaps one of your players.
I hope you have good luck on your next matches, Fabio. Bye!
I hope you have good luck on your next matches, Fabio. Bye!

If you're interested in learning more about this topic, you can visit any of this wonderful articles: Randomized response approach to sensitive issues in surveys, Randomized Response Techniques for Multiple Sensitive Attributes, Design and Analysis of the Randomized Response Technique, Sensitive Questions in Online Surveys.
Below this lines you will find other links, for if you liked this story and you want to share it with your friends.
And don't forget to take a walk by the 123th Carnival of Mathematics. There you'll find lots of excellent math posts that you'll surely like too.














No comments :
Post a Comment