
FIRST HALF
(This entry participates on the 104th edition of the Carnival of Mathematics hosted by Math-Frolic!)
Zlatan Ibrahimovic is sad, very sad. This is because he thinks he has few friends among his teammates.
Zlatan Ibrahimovic is sad, very sad. This is because he thinks he has few friends among his teammates.
When he takes a look at his companions, he realizes that most of his friends have more friends than him. And not only in the pitch or in the locker room, but they also have more followers and friends in social networks (Facebook , Twitter, Linkedin, Google+...).
 He has proposed himself the firm intention to change this situation, and he's looking for someone to give him advice on how to make more friends. So he meets with Thiago Silva at Les Deux Magots to have breakfast and talk about it.
He has proposed himself the firm intention to change this situation, and he's looking for someone to give him advice on how to make more friends. So he meets with Thiago Silva at Les Deux Magots to have breakfast and talk about it. It 's a lovely day in Paris, so Zlatan and Thiago sit outside to have a nice breakfast. Zlatan exposes the problem to Thiago:
It 's a lovely day in Paris, so Zlatan and Thiago sit outside to have a nice breakfast. Zlatan exposes the problem to Thiago:
My friends seem so much more popular than me. I've noticed that they've got more friends, and I'd like to do anything to have so many friends as them.
Thiago Silva talks as follows:
You shouldn’t worry about what you’re saying. It's very common, it's not your fault, it's just Maths.
Do you think that it’s also the fault of Mathematics? Think a moment, and pass to see the solution in the second half.
SECOND HALF
Well, as Thiago Silva says, it’s a simple mathematical problem, and not otherwise. Let's see how Thiago explains it to Ibra:
Do you know the friendship paradox? According to it, your friends have more chances of having more friends than you do...
Well, once I heard that people usually are more likely to be friends with those people who have many friends than with those with few friends ...
Yes, that’s what Satoshi Kanazawa psychologist said: people use to establish friendship more often with people who have many friends that with those which have few. Although it doesn’t match exactly with this problem; we should rather look at the studies of Feld sociologist.
Is this Feld the one who discovered the friendship paradox?
Yes. Indeed, Feld’s frienshid paradox is a property of Graph Theory, by which it’s established that it’s likely that our friends have more friends than we have...
 How is it possible?
How is it possible?
Thiago picks up a notebook and begins to put on paper all the team’s friendship relations.
Let's see it graphically. We’ll write in this paper the 11 lineup players (list on the right).
Now, we'll identify the players with a blue circle (vertices), and we'll write inside them their numbers. We'll connect with a red line (edges) the circles of those who are friends.
Now, we'll identify the players with a blue circle (vertices), and we'll write inside them their numbers. We'll connect with a red line (edges) the circles of those who are friends.
Beside each player we'll write in lilac a figure representing the number of friends he has (just counting the number of red lines from his circle). That way we can see graphically all existing friendship relations on the team.
As you can see, you are the blue circle with number 10 inside it. There’re 3 red lines connecting your circle with your 3 friends: Pastore (27), Lucas (29) and Lavezzi (22). That’s why I wrote a lilac color number 3 beside your circle, because you’ve got 3 friends.
As you can see, you are the blue circle with number 10 inside it. There’re 3 red lines connecting your circle with your 3 friends: Pastore (27), Lucas (29) and Lavezzi (22). That’s why I wrote a lilac color number 3 beside your circle, because you’ve got 3 friends.
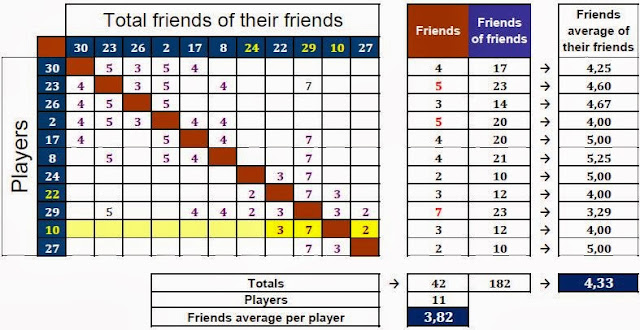
Now we’re going to build a table from this graph. In the line corresponding to each player we’ll write the total of friends of each player’s friends in the cells where his row crosses with his friends' columns. In the table beside, in the first column we’ll put the amount of friends each player has. In the second one we’ll add up all his friends’ friends. And in the third one we’ll calculate the friends average of his friends, by dividing the sum of the friends of the friends by the number of friends.
Let's go first with you, Ibra. You're number 10. Look at row 10: you've got 3 friends: Lavezzi (22), Lucas (29) and Pastore (27). Lavezzi (22) has 3 friends, so we've written a 3 in the cell where your row (10) meets his column (22). Lucas (29) has got 7 friends, so we write a 7 in the cell where your row (10) crosses with his column (29). And Pastore (27) has got 2 friends, so we've written a 2 in the correspondent cell.
We’ll do it that way with all the players, and now we fix our attention to the table on the right.
If we pay our attention to how many players have more friends than the average of their friends, we get, surprisingly, that only 3 of them (23, 2 y 29, in red color) have more friends than the average of their friends (number on third column is greater than number on first column), and the remaining 8 have fewer friends. And as we can see, the total average of the friends
is much lower than the total average of the friends of the friends.
182 / 42 = 4.33
42 / 11 = 3.82
is much lower than the total average of the friends of the friends.
182 / 42 = 4.33
Why does this happen?
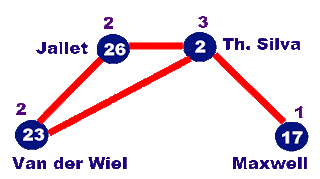
This has to do with the properties of the geometric mean and the statistical variance. Let's take another paper, and we’ll focus only on the friendship relations among the 4 defenders.
We notice that Van der Wiel (23) has got 2 friends, Jallet (26) has 2 friends, Maxwell (17) has got only 1 friend, and I, Thiago (2), have got 3 friends.
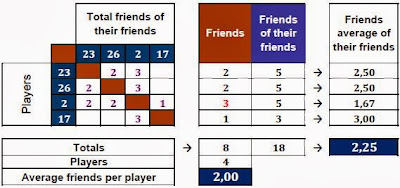
We calculate the friends average of the defenders: (3+2+2+1)/4 = 2. We can see that defenders have 2 friends each one by average.
Now we’ll calculate the friends mean of the defenders’ friends. Van der Wiel (23) has 2 friends, who have 2 and 3 friends, respectively. Jallet (26) has got 2 friends, who have 2 and 3 friends. Maxwell (17) has one friend, who has 3 friends. And I (2) have got three friends, with 2, 2 and 1 friend, respectively.
Thus, we’ve got the following data:
2, 3, 2, 3, 2, 2, 1, 3.
We sort them like this:
3, 3, 3, 2, 2, 2, 2, 1
And we calculate their average:
(3+3+3 + 2+2 + 2+2 + 1) / 8 =
(3·3 + 2·2 + 2·2 + 1·1) / 8 =
(32 + 22 + 22 + 12) / 8 =
2.25
We see how, in a seemingly amazing way, the friends average of defenders’ friends rises up to 2.25, higher than the friends average of defenders we calculated before, which was 2.
That’s true. And always happens the same?
Yes, always. Unless everyone has the same number of friends. In that case the two means are identical.
And why is this happening?
I suppose you've noticed that, when I calculated the mean of friends of friends, I rearranged the data we had in a special order.
2, 3, 2, 3, 2, 2, 1, 3 → 3, 3, 3, 2, 2, 2, 2, 1
Yes, I've noticed it. Why did you do that?
I did it this way so you realized the following question: people who have many friends are incorporated many times within the sum, in fact, so many times as friends they have (3 times number 3), while people who have few friends are included less times (1 time number 1). This means that those players who have more friends have also more weigh in the average (3+3+3+2+2+2+2+1), so that the overall mean tends up.
However, in the friends mean, we add only once each number (3+2+2+1), that is, all people have the same weight, both those who have many friends as those who have few.
I think now I understand it, but I’m not sure that one average has to be larger than the other one for that reason.
Well, then let's go to the mathematical proof.
Let's call xi the number of friends player i has, and μ the friends mean of a n-players team, which will be equal to:
Now let's see how we calculate the friends average of the friends. We’ve seen on the example about the defenders that the sum of the friends of friends corresponds to ∑(xi2), and we know that the amount of friendship relations is ∑xi. So the friends mean of the friends, which we name μ' will be:
For proving this, we’ll use the formula of the statistical variance (σ2) of a discrete random variable. We know that:
It follows like:
We divide both terms by ∑(xi), and we get:

So:
In other words: μ' = μ plus a value greater or equal to zero, because both the statistical variance and the friends average are always non-negative.
Therefore, in a group, the friends average of friends will always be greater than or equal to the average of friends.
Well, with this mathematical demonstration, you definitely convinced me. And beyond the fact that people to not be depressed by having fewer friends than their friends, have all these studies other applications?
Well, this paradox has many applications in many other areas of life. For example, it's used for the control of diseases. Thereby, our club does blood tests to some players to detect any contagious illness and prevent it. Every month they pick 5 players randomly, and does some clinical tests to them. Can you imagine a better way of improving this monitoring task?
No doubt they should pick 5 players randomly, and then ask them each choose a friend. We know these friends of friends have a friends average higher than the initially chosen players, so they’ll also have a much higher chance of being infected, because as they have more friends they are more exposed to infection. This way we get a sample of players more significant than randomly selected.
That's what I was thinking.
t
That’s the way most schools, hospitals or residential homes use to do their sanitary controls. Other application is for people who go to a gym and lose heart because they see that most people are in better shape than them... This doesn’t happen to us, right Ibra? In this case they should realize that when they take a look at the people who are at the gym, they are extracting a biased sample, since it’s likely that people they see are those who spend more hours there, and consequently are in better physical condition.
 It would be better than they approach a few children randomly selected, and ask them to submit to their friends, because then they’ll meet the most popular children of the school, who have more contacts and are more likely to have those missing stickers. Even though they should take care of not becoming infected of any contagious illness by them…
It would be better than they approach a few children randomly selected, and ask them to submit to their friends, because then they’ll meet the most popular children of the school, who have more contacts and are more likely to have those missing stickers. Even though they should take care of not becoming infected of any contagious illness by them…
We can also apply this paradox to other things. That way, it’s a very useful technique for children who collect photocards of players like us. They may apply the friendship paradox to complete their albums in a better way. Usually, they try to change their repeated cards among his friends. But they almost never achieve to complete their albums.
 It would be better than they approach a few children randomly selected, and ask them to submit to their friends, because then they’ll meet the most popular children of the school, who have more contacts and are more likely to have those missing stickers. Even though they should take care of not becoming infected of any contagious illness by them…
It would be better than they approach a few children randomly selected, and ask them to submit to their friends, because then they’ll meet the most popular children of the school, who have more contacts and are more likely to have those missing stickers. Even though they should take care of not becoming infected of any contagious illness by them…
And you can also understand why, when we go in vacation to the beach, we find that it's usually crowded. What about those empty beaches in the brochures? Once again, it’s very likely that the beach we go is full of people, and not completely deserted, because of this paradox.
Not at all. You can see that it happens everywhere. Not only in the Paris Saint Germain, but in all teams: Real Madrid, AC Milan, Manchester United, L.A. Galaxy, Santos, FC Barcelona... And it happens to most players: Cristiano Ronaldo, Neymar, Falcao, Messi ...
Oh, really…? -Ibra asked flashing a shy smile-. I think after these explanations, and as far as it’s lunch time, I should invite you to have lunch at a restaurant a know...
That’s right. But, if you are interested in the friendship paradox, you can write down these other links: 'Why your friends have more friends than you' on Mind your decisions, 'What makes you think you're so popular?' of Zuckerman and Jost, 'The friendship paradox' of Jackson (Guannan) Lu.





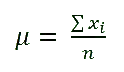

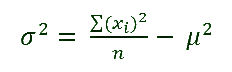


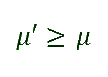


No comments :
Post a Comment